Problem Description
Given an m x n matrix. If an element is 0, set its entire row and column to 0. Do it in-place.
Follow up:
- A straight forward solution using O(mn) space is probably a bad idea.
- A simple improvement uses O(m + n) space, but still not the best solution.
- Could you devise a constant space solution?
Example 1:
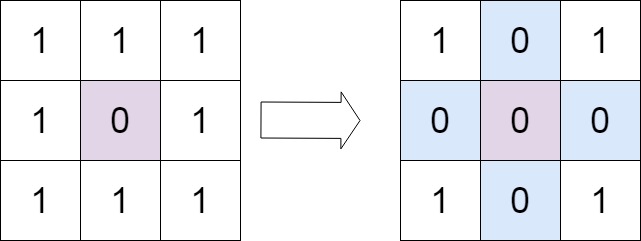
Input: matrix = [[1,1,1],[1,0,1],[1,1,1]] Output: [[1,0,1],[0,0,0],[1,0,1]]
Example 2:
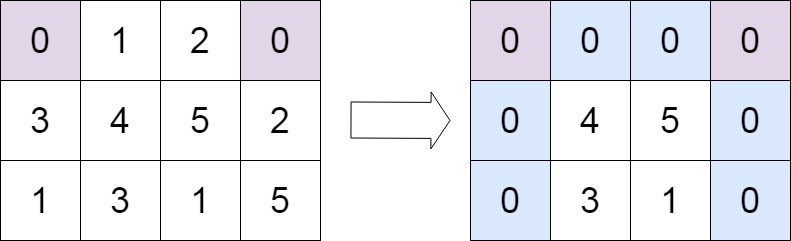
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]
Constraints:
m == matrix.lengthn == matrix[0].length1 <= m, n <= 200-2^31 <= matrix[i][j] <= 2^31 - 1
The description was taken from https://leetcode.com/problems/set-matrix-zeroes/.
Problem Solution
#O(M*N) Time, O(1) Spaceclass Solution: def setZeroes(self, matrix: List[List[int]]) -> None: col_zero = False rows = len(matrix) columns = len(matrix[0]) for row in range(rows): if matrix[row][0] == 0: col_zero = True for col in range(1, columns): if matrix[row][col] == 0: matrix[0][col] = 0 matrix[row][0] = 0 for row in range(1, rows): for col in range(1, columns): if matrix[row][0] == 0 or matrix[0][col] == 0: matrix[row][col] = 0 if matrix[0][0] == 0: for col in range(columns): matrix[0][col] = 0 if col_zero: for row in range(rows): matrix[row][0] = 0Problem Explanation
A good approach is to have two HashSets, one for columns and one for rows. We'd traverse the matrix once and if we saw an element that was a zero then we would append both indices to the sets. We'd traverse once more and update the appropriate columns and rows to zeros.
For the optimal constant space approach that is mentioned in the problem description, we can do this in two traversals.
The first traversal will be to find zeros then set the first element of the corresponding row and column of the cell to zero. Each cell of the first row and column will act as a flag for whether or not each cell within its row or column should also be set to zero and we can make this lookup in constant time once we have the flags.
The second traversal will be through every cell that is not in the first row and column to see if the first element of the row or column was set to zero. If that is the case, we would update the current cell to zero.
In this approach, we want to have a separate variable for setting the first column to zero.
For example, if we have a zero somewhere in the first row but nowhere in the first column and we set a flag that the first row needs to be set to zeros, that would also set a false flag that the first column would be set to zeros.
To handle this, we will skip setting a flag at any cell within the first column during our first traversal but instead, set a separate flag to true if we see a zero in the first column which will let us know whether we'll need to fill the first column as well after we have filled in the rest of the matrix.
We will use this boolean value as a separate flag for the first column. This way, if we do find a zero in the first row then we can utilize matrix[0][0] as the flag for whether the first row needs to be set to zero and won't have to worry about the false positive of the first column.
col_zero = False
Let's set variables for the length of the rows and columns.
rows = len(matrix) columns = len(matrix[0])
Now let's begin our initial traversal to look for zeros and set the first index of the corresponding row and column to zero if we find one. Since it is a matrix, we will need to have two loops that we will use for our traversal.
We will make the first to iterate through the rows.
for row in range(rows):
If we come across a zero element within the first column, we will set the col_zero flag.
if matrix[row][0] == 0: col_zero = True
We will then make the second loop to iterate through the columns, skipping the first one because we just checked for that in the previous step after arriving at the new row.
for col in range(1, columns):
During each iteration, if we come across a zero element then we will set the first element of the corresponding row and column to zero.
if matrix[row][col] == 0: matrix[0][col] = 0 matrix[row][0] = 0
We will traverse the matrix once more starting from the second row and column.
During each iteration, if our current element has a zero as the first cell of its row or column, we will set the cell to zero as well.
for row in range(1, rows): for col in range(1, columns): if matrix[row][0] == 0 or matrix[0][col] == 0: matrix[row][col] = 0
Next, we will see if we need to update the first row to be all zeros.
If the first cell is zero within the matrix, we will set the rest of the row to zero.
if matrix[0][0] == 0: for col in range(columns): matrix[0][col] = 0
Lastly, we will see if we need to update the first column to be all zeros.
If the col_zero value was set to true then we will fill in the first column with zeros.
if col_zero: for row in range(rows): matrix[row][0] = 0