Problem Description
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:
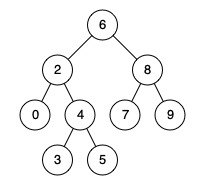
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 Output: 6 Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 Output: 2 Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Example 3:
Input: root = [2,1], p = 2, q = 1 Output: 2
Constraints:
- The number of nodes in the tree is in the range
[2, 10^5]. -10^9 <= Node.val <= 10^9- All
Node.valare unique. p != qpandqwill exist in the BST.
Description taken from https://leetcode.com/problems/invert-binary-tree/.
Problem Solution
#Iterative BFS#O(N) Time, O(N) Spaceclass Solution: def invertTree(self, root: TreeNode) -> TreeNode: if not root: return None queue = collections.deque() queue.append(root) while queue: node = queue.popleft() node.left, node.right = node.right, node.left if node.left is not None: queue.append(node.left) if node.right is not None: queue.append(node.right) return root#Recursive DFS#O(N) Time, O(N) Spaceclass Solution: def invertTree(self, root: TreeNode) -> TreeNode: if not root: return None left = self.invertTree(root.left) right = self.invertTree(root.right) root.left, root.right = right, left return root
Problem Explanation
Iterative Solution
We can solve this problem by implementing a Breadth-First Search for a level order traversal to swap the children of each node.
This will be us swapping from the top down instead of the recursive solution which will be us swapping from the bottom-up.
If the root is null, we have nothing to invert so we will return none.
if not root: return None
Otherwise, let's start by initializing our queue and appending our root to it.
queue = collections.deque() queue.append(root)
We will then create a loop that will run while the queue still has nodes that we need to swap the children for.
while queue:
During each iteration, we will pop a node from the queue and swap its children.
node = queue.popleft() node.left, node.right = node.right, node.left
We will then toss each child of the node into the queue if they are not null so that we can visit them at the next level.
if node.left is not None: queue.append(node.left) if node.right is not None: queue.append(node.right)
Once we have swapped each child through our queue, we will return the root of the tree.
return root
Recursive Solution
With the recursive solution, we will still be swapping the children using a postorder traversal.
This is mostly so that we can reuse the input function, this could be done with a preorder traversal as well but we would need to return the root in a separate function once we have returned from the DFS.
During each recursive call, if we have reached a null node, we will return none.
if not root: return None
We will also call the invertTree function on the left and right child of the current call's node.
left = self.invertTree(root.left) right = self.invertTree(root.right)
At the end of each call that doesn't have a null node, we will set the node's left and right children as the result of the right and left recursive calls. This recursively swaps the children of each node.
root.left, root.right = right, left return root