Lowest Common Ancestor of a Binary Search Tree

Patrick Leaton
Published: April 5, 2021, 5:24 a.m.
Problem Description

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

 

Example 1:

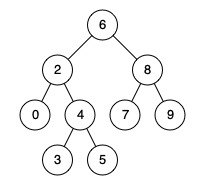
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [2,1], p = 2, q = 1
Output: 2

 

Constraints:

  • The number of nodes in the tree is in the range [2, 10^5].
  • -10^9 <= Node.val <= 10^9
  • All Node.val are unique.
  • p != q
  • p and q will exist in the BST.

 

The description was taken from https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/.

Problem Solution

#Iterative
#O(N) Time, O(1) Space
class Solution:
    def lowestCommonAncestor(self, root:'TreeNode', p:'TreeNode', q:'TreeNode') -> 'TreeNode':
        current = root
        while current:
            if p.val > current.val and q.val > current.val:
                current = current.right
            elif p.val < current.val and q.val < current.val:
                current = current.left
            else:
                return current
 
#Recursive
#O(N) Time, O(N) Space
class Solution:
    def lowestCommonAncestor(self, root:'TreeNode', p:'TreeNode', q:'TreeNode') -> 'TreeNode':
        if p.val > root.val and q.val > root.val:
            return self.lowestCommonAncestor(root.right, p, q)
        elif p.val < root.val and q.val < root.val:
            return self.lowestCommonAncestor(root.left, p, q)
        else:
            return root

 

Problem Explanation

Iterative Solution 

We can utilize the properties of a BST to find the lowest common ancestor.  We won't even need a stack, we can do this in constant time by having a pointer that we will use to traverse the tree.  If the node at the current pointer is less than the two given nodes, we will go to the left child.  If the node at the current pointer is greater than the two given nodes, we will go to the right child.  Otherwise, we are at the lowest common ancestor of the two given nodes so we will return it.

Let's start off by setting our current pointer at the root.

        current = root

 

While the current pointer hasn't reached a null node, we will compare both p and q values with its value.

If both of the p and q values are greater than the current value, then we know that the lowest common ancestor is somewhere on the right side of the tree.  We will move our pointer to the right child.

        while current:
            if p.val > current.val and q.val > current.val:
                current = current.right

 

If both of the p and q values are less than the current value, then we know that the lowest common ancestor is somewhere to the left of the tree.  We will move our pointer to the left child.

            elif p.val < current.val and q.val < current.val:
                current = current.left

 

If one value is greater than or equal to the current value and one value is lower than or equal to the current value, then we are at the lowest common ancestor and we can return our current node.

            else:
                return current

Recursive Solution

The recursive solution is the same idea as the iterative one.

While each recursive call hasn't reached the lowest common ancestor, we will compare both p and q values with the current call's node value.

If both of the p and q values are greater than the current node's value, then we know that the lowest common ancestor is somewhere on the right side of the tree.  We will call our function on the current node's right child.

        if p.val > root.val and q.val > root.val:
            return self.lowestCommonAncestor(root.right, p, q)

 

If both of the p and q values are less than the current node's value, then we know that the lowest common ancestor is somewhere on the left side of the tree.  We will call our function on the current node's left child.

        elif p.val < root.val and q.val < root.val:
            return self.lowestCommonAncestor(root.left, p, q)

 

If one value is greater than or equal to the current node's value and one value is less than or equal to the current node's value, then we are at the lowest common ancestor and we can return our current call's node.

        else:
            return root