Trim a Binary Search Tree

Patrick Leaton
Published: March 30, 2021, 2:27 a.m.
Problem Description

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

 

Example 1:

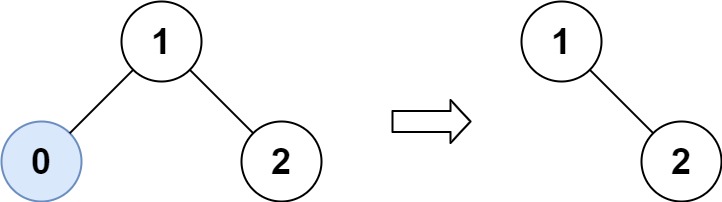
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Example 2:

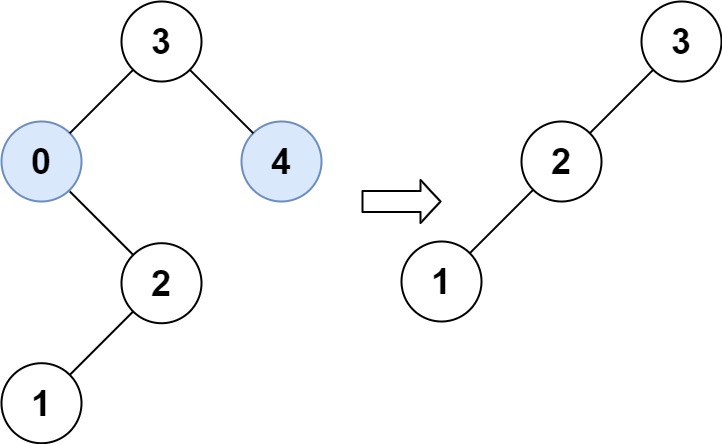
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]

Example 3:

Input: root = [1], low = 1, high = 2
Output: [1]

Example 4:

Input: root = [1,null,2], low = 1, high = 3
Output: [1,null,2]

Example 5:

Input: root = [1,null,2], low = 2, high = 4
Output: [2]

 

Constraints:

  • The number of nodes in the tree in the range [1, 10^4].
  • 0 <= Node.val <= 10^4
  • The value of each node in the tree is unique.
  • root is guaranteed to be a valid binary search tree.
  • 0 <= low <= high <= 10^4

 

The description was taken from https://leetcode.com/problems/trim-a-binary-search-tree/.

Problem Solution

#O(N) Time, O(N) Space
class Solution:
    def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
        def trim(node: TreeNode) -> TreeNode:
            if node is None:
                return None
            elif node.val > high:
                return trim(node.left)
            elif node.val < low:
                return trim(node.right)
            else:
                node.left = trim(node.left)
                node.right = trim(node.right)
                return node
        return trim(root)

Problem Explanation

Binary Search Trees contain an easily searchable structure, if the current node value is less than the target then go left, if it is greater then go right.

By utilizing this structure, we can traverse the tree using a postorder traversal to trim each child edge before returning back to each parent node.

If we encounter a node that is greater than the upper bound, we will return its left child.  If it is less than the lower bound, we will return its right child.  The way we can trim the out of bound nodes is by not returning them within our Depth-First Search traversal.

Let's set our base case so that our Depth-First Search doesn't run infinitely.

If we have gotten a null root input or have traversed to a null node, we will return none.

            if node is None:
                return None

 

If the current node in our function call has a value that is greater than the high value, we can abandon the entire right side of this node's subtree because all of the right children will also be out of bounds.  

If this is the case, we will run the trim function on the left child.  This trims the right children.

            elif node.val > high:
                return trim(node.left)

 

If the current node in our function call has a value that is less than the low value, we can abandon the entire left side of this node's subtree because all of the left children will also be out of bounds.  

If this is the case, we will run the trim function on the right child.  This trims the left children.

            elif node.val < low:
                return trim(node.right)

 

If the current node in our function call is in bounds, we can keep this node and not trim it but will need to continue our trimming DFS on both children before doing so.  This will allow us to trim nodes from the bottom up so that the valid descendent relationships stay intact.

            else:
                node.left = trim(node.left)
                node.right = trim(node.right)
                return node

 

Once we have finished our recursive calls and have returned all valid elements, we will return the root of the tree.

        return trim(root)