Problem Description
Given an m x n integers matrix, return the length of the longest increasing path in matrix.
From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).
Example 1:
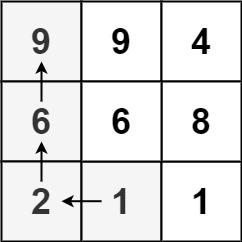
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].
Example 2:
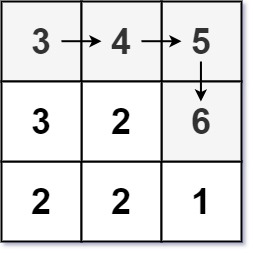
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.
Example 3:
Input: matrix = [[1]] Output: 1
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 2000 <= matrix[i][j] <= 2^31 - 1
The description was taken from https://leetcode.com/problems/longest-increasing-path-in-a-matrix/.
Problem Solution
#O(M*N) Time, O(M*N) Space
class Solution:
def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
m, n = len(matrix), len(matrix[0])
indegrees = [[0] * n for rows in range(m)]
neighbors = [(0,1),(1,0),(-1,0),(0,-1)]
queue = collections.deque()
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >=n:
return False
return True
def bfs() -> int:
path = 0
while queue:
width = len(queue)
for _ in range(width):
row, col = queue.popleft()
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
if matrix[next_row][next_col] > matrix[row][col]:
indegrees[next_row][next_col] -= 1
if not indegrees[next_row][next_col]:
queue.append((next_row, next_col))
path += 1
return path
for row in range(m):
for col in range(n):
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
if matrix[next_row][next_col] < matrix[row][col]:
indegrees[row][col] += 1
for row in range(m):
for col in range(n):
if not indegrees[row][col]:
queue.append((row, col)) return bfs()Problem Explanation
In the problem Longest Consecutive Sequence we found that the most optimal way to find the longest increasing contiguous sequence is to only begin our search from the first potential element of a sequence. We would do this by only beginning the sequence search on an element that had no predecessor within the list.
That is the same intuition we could apply here.
If we look at the paths given in the examples, they form a sort of directed graph. What we can do is make one initial scan through the matrix and for each cell, we will look for neighbors that are greater than the given cell. If we find any, then we will increment that greater neighbor's indegrees count, which is a mapping to each cell node that lets us know how many other cell nodes are pointing to it within the graph.
Once we have created these indegree mappings, we will just need to do one more scan to perform a Breadth-First Search on the initial leaf nodes which would be the nodes that have no indegrees, meaning they have no predecessor within their sequence. This method of traversing parentless or childless nodes within each layer is known as a Topological Sort.
Let's start by saving the length and width of the matrix to variables m, and n so that we don't have to keep rewriting these later.
m, n = len(matrix), len(matrix[0])
Next, we will create an indegrees mapping for each cell in the matrix with an initial value of zero for each indegree count.
indegrees = [[0] * n for rows in range(m)]
We'll also want a list of delta neighbor coordinates so that we can calculate the four surrounding neighbors for each cell.
neighbors = [(0,1),(1,0),(-1,0),(0,-1)]
Lastly, we'll make a queue for our BFS.
queue = collections.deque()
Let's make a helper function that lets us know if the current cell we are about to visit is in the bounds of the array.
If the cell is outside the bounds then the function will return false, otherwise, it will return true.
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >=n:
return False
return True
Now let's make our BFS function.
Remember that prior to this BFS function being run, we will have filled the indegree mapping for each cell node.
def bfs() -> int:
We'll have a path counter which we will increment after traversing each additional layer of our queue.
path = 0
While the queue still has cell nodes to traverse, we will continue our search for the longest path.
while queue:
We'll start each iteration by taking the width of the queue.
This will let us know how many nodes are in the current layer. At the start of our BFS, the first layer of our queue may have multiple root nodes to their increasing path sequences.
| 9 | 9 | 4 |
| 6 | 6 | 8 |
| 2 | 1 | 1 |
Each layer we traverse will be an additional node in their sequence graphs so we just need to count how many layers we traversed to find the longest increasing path.
| 9 | 9 | 4 |
| 6 | 6 | 8 |
| 2 | 1 | 1 |
width = len(queue)
For each node in the current layer, we will pop them from the queue and look at their neighbors, if they're in bounds.
for _ in range(width):
row, col = queue.popleft()
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
Here is where we will need to make a small tweak to a graph Topological Sort so that a matrix Topological Sort will be viable.
In a graph topological sort, after visiting each node we will look at each neighbor node that node has, then decrement their indegrees by one since we are removing the current node from our search and they'll now have one less node pointing to them. Here, just because an adjacent cell is a neighbor, it doesn't mean that it is a neighbor in our search per se.
To account for this, we'll need to make sure that the neighbor cell is also greater than the current one so that we know it belongs to the path we're traversing.
If it is, then we will decrement that neighbor's indegrees by one and if it is now a leaf node, we will add it to the next layer to be visited.
if matrix[next_row][next_col] > matrix[row][col]:
indegrees[next_row][next_col] -= 1
if not indegrees[next_row][next_col]:
queue.append((next_row, next_col))
Each time we traverse an additional path, we'll increment our path variable.
path += 1
Once we have traversed each layer of our candidate paths, we will return the path count which will let us know how many nodes were in the longest increasing path.
return path
Okay, so now we need to fill the indegree mapping.
We'll traverse the matrix and look at each neighbor node that is in bounds. If a neighbor node is greater than the current node then we will increment the neighbor's indegrees by one since we could extend a path from the current node to the neighbor.
for row in range(m):
for col in range(n):
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
if matrix[next_row][next_col] < matrix[row][col]:
indegrees[row][col] += 1
Now that our indegree mappings are filled, we'll find the root nodes for each increasing path by looking for any cells that have no indegrees.
Those will be our first layer to traverse.
for row in range(m):
for col in range(n):
if not indegrees[row][col]:
queue.append((row, col))
Now that everything is in place, we will just need to run our BFS and return the result.
return bfs()