Problem Description
You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.
To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.
Return the maximum number of points you can achieve.
abs(x) is defined as:
xforx >= 0.-xforx < 0.
Example 1:
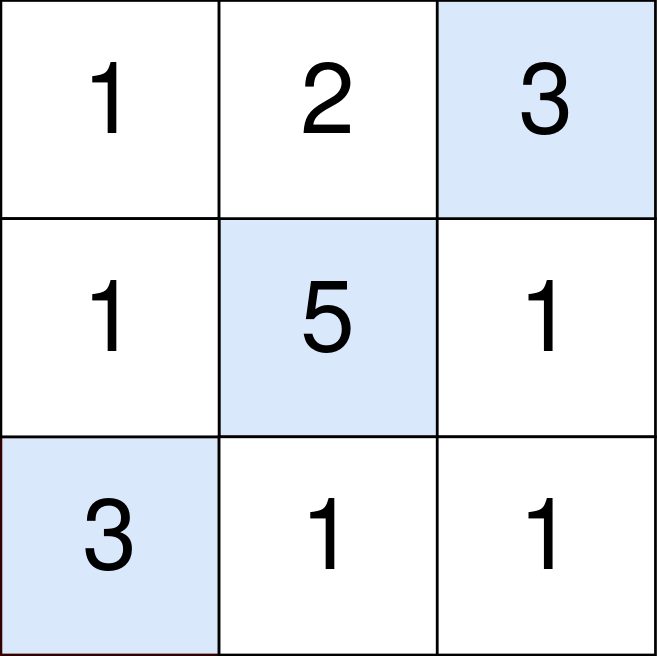
Input: points = [[1,2,3],[1,5,1],[3,1,1]] Output: 9 Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0). You add 3 + 5 + 3 = 11 to your score. However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score. Your final score is 11 - 2 = 9.
Example 2:
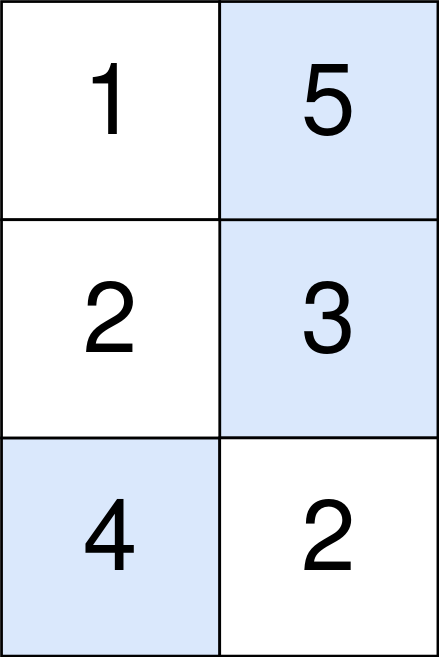
Input: points = [[1,5],[2,3],[4,2]] Output: 11 Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0). You add 5 + 3 + 4 = 12 to your score. However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score. Your final score is 12 - 1 = 11.
Constraints:
m == points.lengthn == points[r].length1 <= m, n <= 10^51 <= m * n <= 10^50 <= points[r][c] <= 10^5
The description was taken from https://leetcode.com/problems/maximum-number-of-points-with-cost/.
Problem Solution
#O(M*N) Time, O(M*N) Space
class Solution:
def maxPoints(self, points: List[List[int]]) -> int:
m, n = len(points), len(points[0])
dp = points.copy()
for row in range(1, m):
prefix, suffix = [0]*n, [0]*n
left_max, right_max = 0, 0
left, right = 0, n-1
while left <= n-1 and right >= 0:
left_max = max(left_max - 1, points[row-1][left])
right_max = max(right_max - 1, points[row-1][right])
prefix[left] = left_max
suffix[right] = right_max
left += 1
right -= 1
for col in range(n):
dp[row][col] += max(prefix[col], suffix[col])
return max(dp[-1])
Problem Explanation
This problem falls into the category of finding paths, similar problems include Minimum Path Sum, Minimum Falling Path Sum, Paint House, Unique Paths, and Triangle.
To solve these types of problems, we'll arrive at point B and bring over the information from each point A that we could have traveled therefrom, based on the overall problem we are trying to solve. If the overall problem is trying to find the maximum path traveling through each row for the matrix, then we can break the overall problem into subproblems by trying to find the maximum path from the previous row to each cell in the current row. Each cell will be each individual subproblem.
However, this problem is much more tricky than the previously aforementioned problems because if we arrive at point B then our point A could be any cell from the previous row since the paths aren't strictly adjacent. That means that if we were to go with a brute force solution then we would be trying to find a maximum pair sum between the current cell and each previous cell minus the distance, which would yield an O(M*N^2) time complexity.
If we ever arrive at a problem where we are recalculating ranges, we can consider implementing a prefix sum array. We will utilize two for each row, one moving from left to right and the other moving right to left. That is how we can solve this problem and drop that time complexity down to O(M*N).
Let's start by saving the length and width of the matrix to values m, and n, so that we don't have to keep rewriting these later.
m, n = len(points), len(points[0])
We'll also want to make a copy of the matrix to build off of.
Technically we could perform this algorithm in place, but it's generally best practice to not do that for concurrency reasons.
dp = points.copy()
Now for each row in the matrix, starting from the second, we will build a prefix sum and a suffix sum array from the previous row so that we may make our point A choice for each point B in the current row.
for row in range(1, m):
These prefix arrays won't have really be containing the prefix "sums" but rather, they will help us find the maximum values at each point with the distance penalty applied.
We could build these using two loops, but we can also do it through one and two pointers.
Let's initialize our arrays, our running maxes, and our two pointers.
prefix, suffix = [0]*n, [0]*n
left_max, right_max = 0, 0
left, right = 0, n-1
While the left pointer hasn't moved past the end of the previous row and the right pointer hasn't moved past the beginning, we will continue building our arrays.
while left <= n-1 and right >= 0:
Okay, now we will start setting the values.
We'll compare our left and right maxes with what they currently are, minus one to account for an additional index traveled, and the current values at their respective pointers within the previous row. Initially, this will set the maxes to a negative one so that they are automatically overwritten with the first values they are compared with.
left_max = max(left_max - 1, points[row-1][left])
right_max = max(right_max - 1, points[row-1][right])
Once we have done that, we'll update the respective indices in the pointers' respective arrays to their respective maxes.
prefix[left] = left_max
suffix[right] = right_max
Then, we'll move the pointers inward.
left += 1
right -= 1
Now that we have built our prefix and suffix arrays from the previous row, we'll have the best value-per-distance in each left cell through the prefix array, each right cell through the suffix array, or one or the other if the best value is directly above.
We'll get that max value then increment the current cell with it, carrying this choice down to the bottom row each time we do this.
for col in range(n):
dp[row][col] += max(prefix[col], suffix[col])
When we have carried each choice to the bottom row, we'll just have to return the maximum value in it.
return max(dp[-1])
Additional Notes
Since we are only utilizing the previous row for each subproblem, each row therebefore will be a waste of space.
We can drop this space complexity down to linear by only having two rows at a time.
To do this, we will initialize the last row as the first row in the matrix. Then, we will initialize an empty row before we begin our traversal of each row. Once we are done building the new row at the end of each row traversal, we will set the new row as the last row. This way, we are only saving the last row in memory for each row traversal while we're building each new row.
#O(M*N) Time, O(N) Space
class Solution:
def maxPoints(self, points: List[List[int]]) -> int:
m, n = len(points), len(points[0])
last_row = points[0]
for row in range(1, m):
new_row = [0] * n
prefix, suffix = [0]*n, [0]*n
left_max, right_max = 0, 0
left, right = 0, n-1 while left <= n-1 and right >= 0:
left_max = max(left_max - 1, last_row[left])
right_max = max(right_max - 1, last_row[right])
prefix[left] = left_max
suffix[right] = right_max
left += 1
right -= 1
for col in range(n):
new_row[col] = points[row][col] + max(prefix[col], suffix[col])
last_row = new_row
return max(last_row)