Problem Description
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
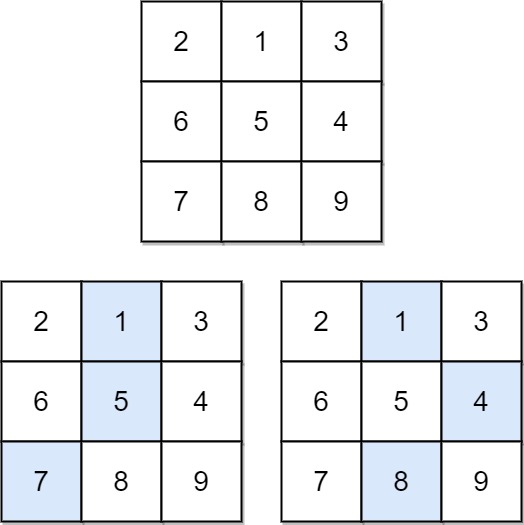
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]] Output: 13 Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
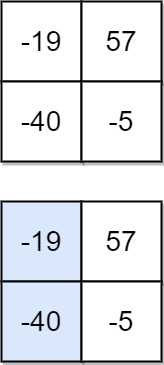
Input: matrix = [[-19,57],[-40,-5]] Output: -59 Explanation: The falling path with a minimum sum is shown.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
The description was taken from https://leetcode.com/problems/minimum-falling-path-sum/.
Problem Solution
#O(N^2) Time, O(N^2) Space
class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
n = len(matrix)
dp = matrix.copy() for row in range(1, n):
for col in range(n):
if col == 0:
dp[row][col] += min(dp[row-1][col], dp[row-1][col+1])
elif col == n - 1:
dp[row][col] += min(dp[row-1][col], dp[row-1][col-1])
else:
dp[row][col] += min(dp[row-1][col-1], dp[row-1][col], dp[row-1][col+1])
return min(dp[-1])Problem Explanation
This problem falls into the category of finding paths, similar problems include Minimum Path Sum, Paint House, Unique Paths, and Triangle.
To solve these types of problems, we'll arrive at point B and bring over the information from each point A that we could have traveled therefrom, based on the overall problem we are trying to solve. If the overall problem is trying to find the minimum contiguous path, for the matrix, then we can break the overall problem into subproblems by trying to find the minimum contiguous path to each cell. Each cell will be each individual subproblem.
Each subproblem will fall into three subcategories:
It is a left cell in which case the only contiguous subpath we could have gotten therefrom would be the cell directly above it or the cell to the upper right.
It is a right cell in which case the only contiguous subpath we could have gotten therefrom would be the cell directly above it or the cell to the upper left.
It is a cell not on any edge in which case the only contiguous subpath we could have gotten therefrom would be the cell directly above it, the upper left, or the upper right.
With that intuition, all we need to do is divide each cell into one of these three categories through conditional statements and continuously find, then tabulate each path. Once we have done that, the minimum path would be carried to the last row.
Let's start by getting the length and width of the input matrix and saving it so that we don't have to keep rewriting this later.
n = len(matrix)
We'll also want to make a copy of the matrix to build off of.
Technically we could perform this algorithm in place, but it's generally best practice to not do that for concurrency reasons.
dp = matrix.copy()
For each row in the matrix starting from the second, since there is no path above the first row, we will go through each column and categorize each subproblem based on the aforementioned explanation.
for row in range(1, n):
for col in range(n):
If the current column is the first, we'll increment the current cell within our dp cache by the minimum value between the top and top-right cells.
if col == 0:
dp[row][col] += min(dp[row-1][col], dp[row-1][col+1])
If the current cell is the last, we'll increment the current cell within our dp cache by the minimum value between the top and top-left cells.
elif col == n - 1:
dp[row][col] += min(dp[row-1][col], dp[row-1][col-1])
Otherwise, we'll increment the current cell within our dp cache by the minimum value between the top-left, the top, and the top-right cells.
else:
dp[row][col] += min(dp[row-1][col-1], dp[row-1][col], dp[row-1][col+1])
Once we have tabulated each path, we will find the minimum one in the last row of our dp cache.
return min(dp[-1])
Additional Notes
Since we are only utilizing the previous row for each subproblem, each row therebefore will be a waste of space.
We can drop this space complexity down to linear by only having two rows at a time.
To do this, we will initialize the last row as the first row in the matrix. Then, we will initialize an empty row before we begin our traversal of each row. Once we are done building the new row at the end of each row traversal, we will set the new row as the last row. This way, we are only saving the last row in memory for each row traversal while we're building each new row.
#O(N^2) Time, O(N) Space
class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
n = len(matrix)
last_row = matrix[0]
for row in range(1, n):
new_row = []
for col in range(n):
if col == 0:
new_row.append(min(last_row[col], last_row[col+1]) + matrix[row][col])
elif col == n - 1:
new_row.append(min(last_row[col], last_row[col-1]) + matrix[row][col])
else:
new_row.append(min(last_row[col-1], last_row[col], last_row[col+1]) + matrix[row][col])
last_row = new_row
return min(last_row)