Problem Description
Given the root of a binary tree where every node has a unique value and a target integer k, return the value of the nearest leaf node to the target k in the tree.
Nearest to a leaf means the least number of edges traveled on the binary tree to reach any leaf of the tree. Also, a node is called a leaf if it has no children.
Example 1:
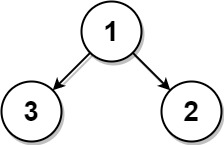
Input: root = [1,3,2], k = 1 Output: 2 Explanation: Either 2 or 3 is the nearest leaf node to the target of 1.
Example 2:

Input: root = [1], k = 1 Output: 1 Explanation: The nearest leaf node is the root node itself.
Example 3:
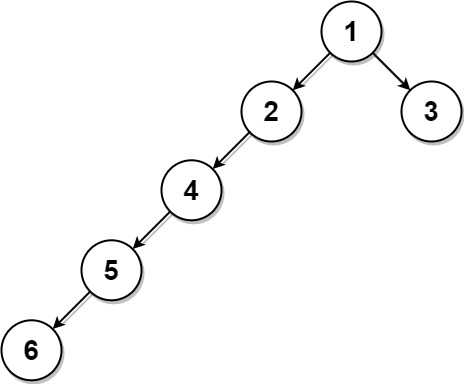
Input: root = [1,2,3,4,null,null,null,5,null,6], k = 2 Output: 3 Explanation: The leaf node with value 3 (and not the leaf node with value 6) is nearest to the node with value 2.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 1 <= Node.val <= 1000- All the values of the tree are unique.
- There exist some node in the tree where
Node.val == k.
The description was taken from https://leetcode.com/problems/closest-leaf-in-a-binary-tree/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def findClosestLeaf(self, root: Optional[TreeNode], k: int) -> int:
adjacency, seen = {root.val:[0]}, {}
def dfs(node:TreeNode, parent:TreeNode) -> None:
if not node:
return
if node.val not in adjacency:
adjacency[node.val] = []
adjacency[parent.val].append(node.val)
adjacency[node.val].append(parent.val)
dfs(node.left, node)
dfs(node.right, node)
def bfs() -> int:
queue = collections.deque([(k)])
while queue:
node = queue.popleft()
if not node:
continue
if len(adjacency[node]) <= 1:
return node
for neighbor in adjacency[node]:
if neighbor not in seen:
seen[neighbor] = True
queue.append(neighbor)
dfs(root.left, root)
dfs(root.right, root)
return bfs()Problem Explanation
This solution is going to be nearly the same as All Nodes Distance K in Binary Tree.
If we look at the examples, we can see that there is no clean way to bring any useful information from the root down to child nodes through a preorder traversal nor is there any way to bring any useful information from each leaf up to the root through a postorder traversal.
If we look at example three, we'll see that we would need to go up, through the root, and down to get from node two to three, or from three to two. That is going to require two directions.
The problem is, a binary tree is a directed graph. It only has downward edges from parent to child. To be able to travel both up and down from node k, the source node, we'll need to create an additional node-to-parent edge. Without trying to mutate the TreeNode class, this can be achieved by performing a Depth-First Search to create an adjacency list, a mapping from each node to its child and parent.
From there, a normal Breadth-First Search can be utilized to find the minimum path to the closest leaf.
Let's start by initializing our adjacency list and our seen dictionary.
The terminating condition within our BFS will be if the current node only has one other node in its adjacency list, its parent, then it is a leaf node and we should return it.
If the root itself is node k, and it has no children, then it is a leaf. That means if we have a tree with a single node, then the root node will have zero nodes in its adjacency list and won't satisfy the aforementioned terminating condition. Also, if we modified the condition to be less than or equal to one node in its adjacency list, and the root had one child node but the root node was node k, then the root would still satisfy that condition when it should have been the child leaf node.
Long story short, we're going to need a dummy parent node for the root within our adjacency list. Since there won't be any node zero within the input according to the given constraints, we'll make the dummy node value a zero.
adjacency, seen = {root.val:[0]}, {}
Now we'll fill our adjacency list with node-to-parent and parent-to-node edges.
We'll perform a preorder DFS to do this.
def dfs(node:TreeNode, parent:TreeNode) -> None:
If the current node is null, we'll return.
if not node:
return
If the current node hasn't been initialized in the adjacency list yet, we'll place it there with an empty array.
if node.val not in adjacency:
adjacency[node.val] = []
Next, we'll place the current node in its parent's adjacency list and vice versa.
adjacency[parent.val].append(node.val)
adjacency[node.val].append(parent.val)
After we have done that, we'll continue our search on both child nodes.
dfs(node.left, node)
dfs(node.right, node)
Next, let's create our BFS helper function.
def bfs() -> int:
We'll initialize our queue with the source node, node k.
queue = collections.deque([(k)])
While we still have nodes in our queue, we will continue our search.
while queue:
Within each iteration, we'll pop a node from the queue.
node = queue.popleft()
If that node is the dummy parent node, then we will continue to the next iteration.
if not node:
continue
Otherwise, we'll check if this is a leaf node.
If it is, we will return it.
if len(adjacency[node]) <= 1:
return node
If not, we'll go through each parent and child neighbor of this node, if these neighbors have not been seen yet then we will mark them as seen and append them to the queue so that we can visit them within the next layer.
for neighbor in adjacency[node]:
if neighbor not in seen:
seen[neighbor] = True
queue.append(neighbor)
Now that we have the dfs and bfs functions built, we'll make the initial DFS calls on the root's left and right children, with the root being the first parent whose value was initialized in the adjacency list at the beginning of the solution.
dfs(root.left, root)
dfs(root.right, root)
Once we have our adjacency list filled, we just need to run our BFS and return the closest leaf node to node k.
return bfs()