Problem Description
Given the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.
A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.
Example 1:
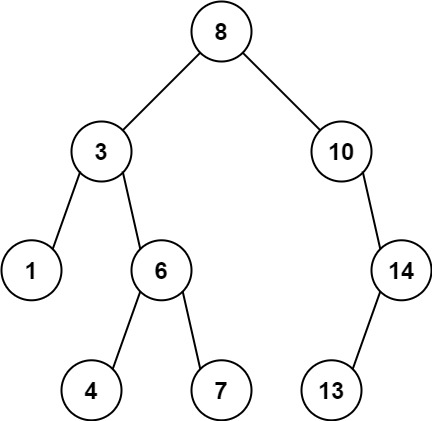
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13] Output: 7 Explanation: We have various ancestor-node differences, some of which are given below : |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Example 2:
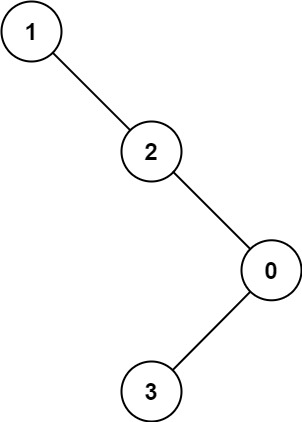
Input: root = [1,null,2,null,0,3] Output: 3
Constraints:
- The number of nodes in the tree is in the range
[2, 5000]. 0 <= Node.val <= 10^5
The description was taken from https://leetcode.com/problems/maximum-difference-between-node-and-ancestor/.
Problem Solution
#DFS#O(N) Time, O(N) Space
class Solution:
def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:
output = 0
def preorder(node:TreeNode, maximum:int, minimum:int) -> None:
nonlocal output
if not node:
return
difference = max(abs(node.val - maximum), abs(node.val - minimum))
output = max(output, difference)
maximum = max(maximum, node.val)
minimum = min(minimum, node.val)
preorder(node.left, maximum, minimum)
preorder(node.right, maximum, minimum)
preorder(root, root.val, root.val)
return output#BFS
#O(N) Time, O(N) Space
class Solution:
def maxAncestorDiff(self, root: Optional[TreeNode]) -> int:
def bfs() -> int:
output = 0
queue = collections.deque([(root, root.val, root.val)])
while queue:
node, maximum, minimum = queue.popleft()
if not node:
continue
difference = max(abs(node.val - maximum), abs(node.val - minimum))
output = max(output, difference)
maximum = max(maximum, node.val)
minimum = min(minimum, node.val)
queue.append((node.left, maximum, minimum))
queue.append((node.right, maximum, minimum))
return output
return bfs()Problem Explanation
Depth-First Search
From the problem description, we may recognize that there are no constraints for whether the ancestor must have a greater or lesser value than its descendant's node value.
Seeing that, we can solve this problem through a DFS where we calculate the greatest absolute difference at each node by finding the absolute differences between itself and the previous minimum and maximum nodes within its upper branch.
Let's start by initializing our output maximum difference to zero.
This would be the base case if all of the nodes in the tree had the same value.
output = 0
Next, let's make our recursive preorder function.
This function will take a tree node to be visited, a maximum node value, and a minimum node value within the current path.
def preorder(node:TreeNode, maximum:int, minimum:int) -> None:
Let's start by declaring to Python that the output variable we are going to reference within this function is nonlocal to the function and its scope is within the outer function so that we don't get an error.
nonlocal output
Otherwise, let's set our base case.
If we have reached a null node then we have exhausted a DFS path and will return from it.
if not node:
return
Next, we will calculate the maximum difference of this node between itself and its ancestors.
We will do this by taking the absolute difference of this node and both the maximum and minimum node we have seen so far within the current path, then taking the maximum between these two differences.
difference = max(abs(node.val - maximum), abs(node.val - minimum))
Once we do that, we will compare this difference with the greatest difference we have saved, updating the saved greatest difference if this one is greater.
output = max(output, difference)
Afterward, we will compare this node's value to the current maximum and minimum in case this node's value is lesser than the minimum or greater than the maximum.
maximum = max(maximum, node.val)
minimum = min(minimum, node.val)
Once we have done that, we will continue the search on this node's children.
preorder(node.left, maximum, minimum)
preorder(node.right, maximum, minimum)
Now that we have our helper function built, all we need to do is make the initial call on the root node with itself as the maximum and minimum then return the output once our DFS has completed.
preorder(root, root.val, root.val)
return output
Breadth-First Search
Converting a preorder DFS to a BFS is typically the easiest type of recursive traversal to convert into an iterative one.
All we need to do is swap out the function call arguments for a tuple with the same variables, swap the call stack out for a queue, and create a loop that runs while the queue still has nodes.
The rest of the logic will be the exact same.
Let's start by creating a BFS helper function.
def bfs() -> int:
We'll need an output variable, similar to the recursive approach.
output = 0
We'll also need a queue.
Each queue element will be a tuple that will contain a tree node, a current maximum within the current path, and a current minimum within the current path.
Let's initialize our queue with the root.
queue = collections.deque([(root, root.val, root.val)])
While the queue still has nodes to traverse, we will continue our search.
while queue:
The rest of this code is the same as the DFS approach.
if not node:
continue
difference = max(abs(node.val - maximum), abs(node.val - minimum))
output = max(output, difference)
maximum = max(maximum, node.val)
minimum = min(minimum, node.val)
queue.append((node.left, maximum, minimum))
queue.append((node.right, maximum, minimum))
Once we have visited each node within the tree, we'll return the maximum difference.
return output
Now that our helper function is built, all we need to do is make the initial call and return the maximum difference.
return bfs()