Problem Description
You are given an m x n matrix maze (0-indexed) with empty cells (represented as '.') and walls (represented as '+'). You are also given the entrance of the maze, where entrance = [entrancerow, entrancecol] denotes the row and column of the cell you are initially standing at.
In one step, you can move one cell up, down, left, or right. You cannot step into a cell with a wall, and you cannot step outside the maze. Your goal is to find the nearest exit from the entrance. An exit is defined as an empty cell that is at the border of the maze. The entrance does not count as an exit.
Return the number of steps in the shortest path from the entrance to the nearest exit, or -1 if no such path exists.
Example 1:
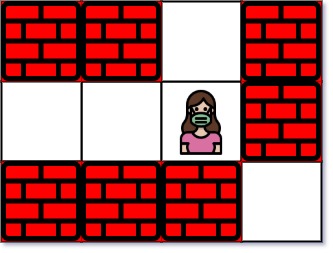
Input: maze = [["+","+",".","+"],[".",".",".","+"],["+","+","+","."]], entrance = [1,2] Output: 1 Explanation: There are 3 exits in this maze at [1,0], [0,2], and [2,3]. Initially, you are at the entrance cell [1,2]. - You can reach [1,0] by moving 2 steps left. - You can reach [0,2] by moving 1 step up. It is impossible to reach [2,3] from the entrance. Thus, the nearest exit is [0,2], which is 1 step away.
Example 2:

Input: maze = [["+","+","+"],[".",".","."],["+","+","+"]], entrance = [1,0] Output: 2 Explanation: There is 1 exit in this maze at [1,2]. [1,0] does not count as an exit since it is the entrance cell. Initially, you are at the entrance cell [1,0]. - You can reach [1,2] by moving 2 steps right. Thus, the nearest exit is [1,2], which is 2 steps away.
Example 3:

Input: maze = [[".","+"]], entrance = [0,0] Output: -1 Explanation: There are no exits in this maze.
Constraints:
maze.length == mmaze[i].length == n1 <= m, n <= 100maze[i][j]is either'.'or'+'.entrance.length == 20 <= entrancerow < m0 <= entrancecol < nentrancewill always be an empty cell.
The description was taken from https://leetcode.com/problems/nearest-exit-from-entrance-in-maze/.
Problem Solution
#O(M*N) Time, O(M*N) Space
class Solution:
def nearestExit(self, maze: List[List[str]], entrance: List[int]) -> int:
m, n = len(maze), len(maze[0])
border_rows = set([0, m-1])
border_cols = set([0, n-1])
seen = {}
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >= n:
return False
if maze[row][col] == "+":
return False
if (row, col) in seen:
return False
return True
def bfs() -> int:
steps = 0
neighbors = [(0,1), (1,0), (0,-1), (-1,0)]
queue = collections.deque([(entrance)])
while queue:
width = len(queue)
for _ in range(width):
row, col = queue.popleft()
if row in border_rows or col in border_cols:
if [row, col] != entrance:
return steps
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
queue.append((next_row, next_col))
seen[(next_row, next_col)] = True
steps += 1
return -1
return bfs()Problem Explanation
In this problem, we are required to do two things: see if a path exists to an exit, and if it does, find the shortest path to an exit.
In both of these use cases, a Breadth-First Search is the favored choice over a Depth-First Search since a BFS will travel outward through multiple layers within a linear fashion where a DFS would travel like a snake in the order of directions listed in its stack and find nonoptimal paths to the exits.
There are a couple of approaches we could take to this problem. We could either traverse the borders of the grid and initialize our queue with each exit and find the nearest path to the entrance, or more intuitively, we could initialize our queue with the entrance and find the nearest path to an exit. The former would be more useful if we had to mark each cell with its distance to the nearest exit like in Walls and Gates but we'll go with the more intuitive approach here.
Let's start by saving the length and width of our queue to the variables m, and n so that we don't have to keep rewriting these values.
m, n = len(maze), len(maze[0])
Next, let's just make a couple of helper sets so that when we find a cell in our search we can see if it is on the border to know whether it is an exit.
If its row coordinate is within the first or last row, or its column coordinate is within the first or last column, we have an exit.
border_rows = set([0, m-1])
border_cols = set([0, n-1])
We'll also need a HashMap or HashSet to know whether a cell has been visited also so that we don't keep revisiting cells and creating cycles within our search.
seen = {}
Let's also create a helper function for us to know whether a cell is in bounds.
The function will take a row and a column coordinate for the cell.
def in_bounds(row:int, col:int) -> bool:
If the current row is outside the bounds of the grid, the cell is a wall, or the cell has already been visited, the function will return false.
if row < 0 or col < 0 or row >= m or col >= n:
return False
if maze[row][col] == "+":
return False
if (row, col) in seen:
return False
Otherwise, it will return true.
return True
Finally, let's make our BFS function.
def bfs() -> int:
Within our search, we will have a steps counter which we will increment after traversing each additional layer.
steps = 0
We'll also have a list of delta coordinates which will let us easily find the four neighbors of each cell.
neighbors = [(0,1), (1,0), (0,-1), (-1,0)]
We'll need a queue as well, which we will initialize with the entrance coordinates.
queue = collections.deque([(entrance)])
While we still have cell nodes in our queue, we will continue searching for an exit.
while queue:
Each iteration will start by us saving the width of the queue as this will let us know how many cells are within the current layer.
width = len(queue)
Then, for each node in the queue, we will pop it from the queue and unpack its row and column.
for _ in range(width):
row, col = queue.popleft()
If the node is on the border, and it isn't the given entrance, we will return the number of steps we took which would be the number of layers we traversed.
if row in border_rows or col in border_cols:
if [row, col] != entrance:
return steps
Otherwise, we will calculate its four neighbors and if they are in bounds according to the conditions we specified in our helper function, we will mark them as seen and push them into the queue to be visited within the next layer.
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
queue.append((next_row, next_col))
seen[(next_row, next_col)] = True
Once we have done this for all the nodes within a layer, we will increment the number of steps that we have taken.
steps += 1
If we have emptied the queue and never found a path to an exit then all of the exits were either blocked off by walls, or the entire maze was just a single cell entrance.
In either case, we will return a negative one.
return -1
Now that our helper functions are built, we just need to make a single call to run our BFS and return the number of steps to the nearest exit.
return bfs()