Deepest Leaves Sum

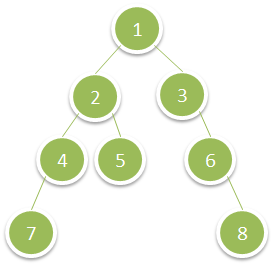
Input: root = [1,2,3,4,5,null,6,7,null,null,null,null,8]
Output: 15

Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 19

---

Recursive Depth-First Search

If we are wanting to group nodes within a tree together based on a specific identifier or constraint, we can easily do that with the implementation of a HashMap.

What we can do is perform a recursive DFS and group all of the nodes together by their depths.  

Once we have done that, all we need to do is return the sum of the nodes that have the maximum depth.

---

Let's start by initializing our dictionary.

Each depth will be the hashing key, and each key will have a list of node values.

        depths = {}

---

Next, we will make our recursive DFS function.

We'll roll with an inorder traversal here but a preorder or postorder traversal should do the trick as well.

Each function call will take a node to be visited and a depth value as arguments.

        def inorder(node:TreeNode, depth:int) -> None:

 

Let's set our base case.

If we hit a null node, then we have exhausted a DFS path so we will return from it.

            if not node:
                return

 

Otherwise, we will continue our DFS on the left child of the current node and increment the depth by one as we are moving down further down to the next level.

            inorder(node.left, depth + 1)

 

Once the DFS yoyo has slung back up to the current node, we will either append the current node's value to the current depth group or initialize the current depth group with the current node's value if it doesn't exist yet within the dictionary.

            if depth not in depths:
                depths[depth] = [node.val]
            else:
                depths[depth].append(node.val)

 

After we have processed the current node, we will continue our DFS on the right child.

            inorder(node.right, depth + 1)

---

Now that our helper function is built, we just need to make the initial call on the root with an initial depth of zero.

Once we have filled our dictionary, we'll return the sum of the maximum depth's node values.

        inorder(root, 0)
        return sum(depths[max(depths.keys())])

---

---

Iterative Breadth-First Search

Another, maybe more intuitive approach is to tackle this problem through the implementation of a level-order traversal.

The deepest leaves will be at the last level, so what we can do is keep a rolling sum that we'd reset before each level and increment during each level traversal.  

By doing this, we will keep the sum of the nodes within the last level.

---

Let's just start by building our bfs function.

        def bfs() -> int:

 

We'll initialize a queue with the root node and our level sum to zero.

            queue = collections.deque([(root)])
            level_sum = 0

 

While we still have nodes in the queue, we still have levels to search.

            while queue:

 

Before we traverse a new level, we will save the width of the queue.  This will let us know how many nodes are at the next level.

                width = len(queue)

 

We'll also reset the level sum so that we aren't carrying over any node values from the previous level.

                level_sum = 0

 

For each node within the current level, we will pop it from the queue, increment the level sum by its value, and if it has children, add them to the queue to be visited next.

                for _ in range(width):
                    node = queue.popleft()
                    level_sum += node.val
                    if node.left:
                        queue.append(node.left)
                    if node.right:
                        queue.append(node.right)

 

After each level has been traversed, the last level sum that was calculated will have been the level of the deepest leaves.

            return level_sum

---

Now that our helper function is built, we just need to make the initial call to run the BFS and return the level sum.

        return bfs()

---