Minimum Operations to Make a Uni-Value Grid

Patrick Leaton
Published: Nov. 27, 2021, 10:17 p.m.
Problem Description

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

 

Example 1:

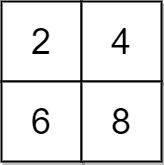
Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.

Example 2:

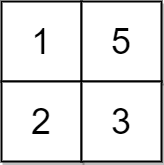
Input: grid = [[1,5],[2,3]], x = 1
Output: 5
Explanation: We can make every element equal to 3.

Example 3:

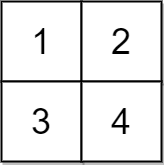
Input: grid = [[1,2],[3,4]], x = 2
Output: -1
Explanation: It is impossible to make every element equal.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 10^5
  • 1 <= m * n <= 10^5
  • 1 <= x, grid[i][j] <= 10^4

 

The description was taken from https://leetcode.com/problems/minimum-operations-to-make-a-uni-value-grid/.

Problem Solution

#O(M*N) Time, O(N) Space
class Solution:
    def minOperations(self, grid: List[List[int]], x: int) -> int:
        nums = []
        output = 0

        for row in range(len(grid)):
            for col in range(len(grid[0])):
                nums.append(grid[row][col])
        nums.sort()
        cheapest = nums[len(nums)//2]

        for num in nums:
            distance = abs(cheapest - num)
            if distance%x != 0:
                return -1
            else:
                output += distance//x

        return output

Problem Explanation

This problem is a greedy problem.

A hint that a question may be a greedy problem is when we are required to find the minimum number of steps to reach a specific goal. 

Similar to other traditional greedy problems, we can solve this by sorting our input, identifying the cheapest or most costly tasks, and prioritizing those so that we may conserve resources.

In this problem, we'll need to make add or subtract some frequency of x to each element for it to become a single number that we choose that exists in the matrix.

Which number should we choose though?

That is where the greedy aspect comes into play.  

We'll want to pick a value that will require the fewest amount of addition operations for smaller numbers to become it and also the fewest amount of subtraction operations for greater numbers to become it.  If we were to sort each element from our grid, that number we'll choose would be smack-dab in the middle of the sorted list.

To reiterate, we can solve this by sorting our input, our grid, identifying the cheapest task, the median value, and prioritizing the operation distance to that task for each element so that we may conserve resources, our operations.

If we encounter an element that cannot be evenly incremented or decremented by x to close the distance between it and the number we choose, we will return a negative one.

Let's start by initializing an empty array that we will place each number from our grid into.

We'll also need an output counter to track the total number of operations we applied.

        nums = []
        output = 0

 

Next, we will traverse the grid and place each value into our array.

        for row in range(len(grid)):
            for col in range(len(grid[0])):
                nums.append(grid[row][col])

 

After we do that, we will sort our array and choose the middle value.   

This is our chosen value that we'll simulate transforming each other value into.

        nums.sort()
        cheapest = nums[len(nums)//2]

 

For each number in our numbers array, we'll calculate the absolute difference between the current number and the cheapest number.  

This is the edit distance between the two.

        for num in nums:
            distance = abs(cheapest - num)

 

If that edit distance is not divisible by x, then there is no amount of addition or subtraction that we could apply to make this grid uni-value.

If this is the case, we will return a negative one.

            if distance%x != 0:
                return -1

 

Otherwise, we will increment our output by the distance divided by x.

This is the number of operations of x we would have to apply to the current number for it to become the cheapest.

            else:
                output += distance//x

 

Once we have calculated the number of operations to transform each number into the cheapest, we will return the output.

        return output