Problem Description
Given the root of a binary tree, return the length of the longest path, where each node in the path has the same value. This path may or may not pass through the root.
The length of the path between two nodes is represented by the number of edges between them.
Example 1:
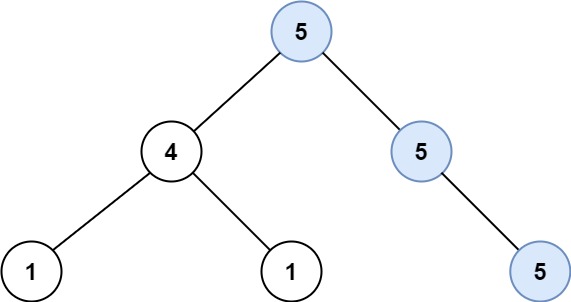
Input: root = [5,4,5,1,1,5] Output: 2
Example 2:
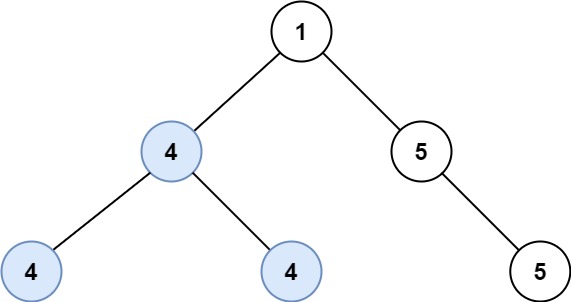
Input: root = [1,4,5,4,4,5] Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 10^4]. -1000 <= Node.val <= 1000- The depth of the tree will not exceed
1000.
The description was taken from https://leetcode.com/problems/longest-univalue-path/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
output = 0
def postorder(node:TreeNode) -> list:
if not node:
return [None, 0]
nonlocal output
left = postorder(node.left)
right = postorder(node.right)
if node.val == left[0]:
left[1] += 1
else:
left[1] = 0
if node.val == right[0]:
right[1] += 1
else:
right[1] = 0
through_node = left[1] + right[1]
output = max(output, through_node)
return [node.val, max(left[1], right[1])]
postorder(root)
return outputProblem Explanation
Let's clear some things up before we get into the explanation.
The description says we are looking for any path, but it fails to mention that we are supposed to look for any single path that doesn't join at a node and continue.
If we had a tree like this:
This would count as a single path because it is a path that is going through a node and not continuing from it.
If the tree was like this, however:
We would have to choose a left or a right path, not both.
Okay, now for the explanation.
The problem is very similar to Diameter of Binary Tree and Binary Tree Maximum Path Sum.
We are looking for a path that may or may not go through the root and will provide the maximum sum possible.
If the path may or may not go through the root, then we won't want to start our search from the root. It'd make more sense to visit it last with a postorder traversal Depth-First Search.
If a path doesn't continue from a node with a conjoined path from its children's paths as mentioned previously, then for comparison purposes, we will want to include each subtree root when testing for the longest path, but only continue each path from the maximum chain between its left and right children.
First off, if we have no root then we couldn't have a univalue path with a length of more than zero.
If this is the case, we will return zero.
if not root:
return 0
Otherwise, we will initialize our output to zero, which will be the base case if there are no two consecutive nodes with the same value.
output = 0
Next, we will make our postorder helper function.
def postorder(node:TreeNode) -> list:
Let's think about what information we need from each child node in order to find the longest univalue path, this will help us set a base case.
If we need to make a path between any two nodes, we are going to need to know if the two nodes are the same. If we try to access the val attribute of the given node class on a null node, then we will get an error. It would be helpful to us if we returned each node's value so that we can avoid doing that.
If we want to continue a path, we are going to also need to know how long that path was before it got to the current node. It would also be helpful for us to return that as well.
Our base case will be if we hit a null node, we will return null for the node value and zero for the longest path up to that node.
if not node:
return [None, 0]
Next, we will need to declare to Python that this output variable exists outside the scope of this inner function.
nonlocal output
If we haven't hit our base case yet, we will continue our DFS on the current node's left and right children.
left = postorder(node.left)
right = postorder(node.right)
If the current node value is the same as the left node's we will increment the left node's path length of univalue nodes by one, otherwise, we will reset it to zero.
if node.val == left[0]:
left[1] += 1
else:
left[1] = 0
We'll do the same for the right child.
if node.val == right[0]:
right[1] += 1
else:
right[1] = 0
For comparison purposes, we will test the longest path including the current node by adding both children's longest paths.
through_node = left[1] + right[1]
output = max(output, through_node)
Since a path can't be joined and continue through the current node, however, we will return the current node value and the maximum between both children's paths.
return [node.val, max(left[1], right[1])]
Now that our helper function is built, we will just need to make the initial call on the root and return the output.
postorder(root)
return output