Problem Description
You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.
You are given an array of employees employees where:
employees[i].idis the ID of theithemployee.employees[i].importanceis the importance value of theithemployee.employees[i].subordinatesis a list of the IDs of the direct subordinates of theithemployee.
Given an integer id that represents an employee's ID, return the total importance value of this employee and all their direct and indirect subordinates.
Example 1:
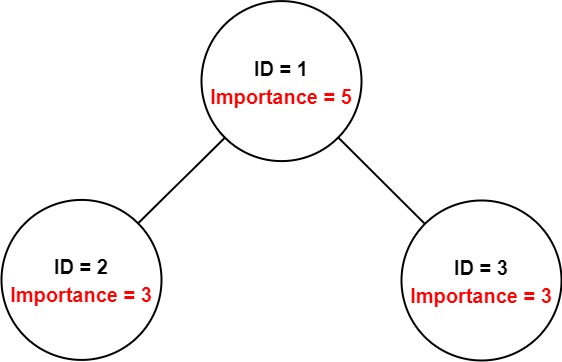
Input: employees = [[1,5,[2,3]],[2,3,[]],[3,3,[]]], id = 1 Output: 11 Explanation: Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3. They both have an importance value of 3. Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.
Example 2:
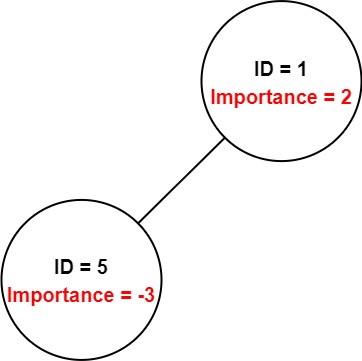
Input: employees = [[1,2,[5]],[5,-3,[]]], id = 5 Output: -3 Explanation: Employee 5 has an importance value of -3 and has no direct subordinates. Thus, the total importance value of employee 5 is -3.
Constraints:
1 <= employees.length <= 20001 <= employees[i].id <= 2000- All
employees[i].idare unique. -100 <= employees[i].importance <= 100- One employee has at most one direct leader and may have several subordinates.
- The IDs in
employees[i].subordinatesare valid IDs.
The description was taken from https://leetcode.com/problems/employee-importance/.
Problem Solution
#BFS
#O(N) Time, O(N) Space
class Solution:
def getImportance(self, employees: List['Employee'], id: int) -> int:
adjacency, importance = {}, {}
output = 0
for employee in employees:
importance[employee.id] = employee.importance
adjacency[employee.id] = employee.subordinates
def bfs(employee:int) -> None:
nonlocal output
queue = collections.deque([(employee)])
while queue:
width = len(queue)
for _ in range(width):
employee = queue.popleft()
output += importance[employee]
for subordinate in adjacency[employee]:
queue.append((subordinate))
bfs(id)
return output#DFS
#O(N) Time, O(N) Space
class Solution:
def getImportance(self, employees: List['Employee'], id: int) -> int:
adjacency, importance = {}, {}
output = 0
for employee in employees:
importance[employee.id] = employee.importance
adjacency[employee.id] = employee.subordinates def dfs(employee:int) -> None:
nonlocal output
output += importance[employee]
for subordinate in adjacency[employee]:
dfs(subordinate) dfs(id)
return outputProblem Explanation
Breadth-First Search
In order to calculate the total importance of an employee, we would need to sum their importance value with the importance value of their immediate subordinates, and all of their indirect subordinates.
This means we can picture the employee we are trying to find the total importance for as the root of a subtree within this overall organization.
To calculate the total importance, we just need to traverse each of the employee's child nodes, and their child nodes, and sum their values as we would for a binary tree.
Let's start by initializing two HashMaps.
One will be to map each employee to their subordinates and the other will be to map each employee with their importance value for constant lookups.
adjacency, importance = {}, {}
We'll also need an output value which will be the overall importance of the input employee.
output = 0
Let's traverse each employee object within this input employees list.
for employee in employees:
For each employee, we will map their importance within our importance dictionary.
importance[employee.id] = employee.importance
We will also map their subordinates to them within our adjacency list.
adjacency[employee.id] = employee.subordinates
Next, we'll make our BFS helper function that will take an employee root node to begin traversal from.
def bfs(employee:int) -> None:
Within the function, we'll first need to declare to Python that this output variable exists outside the scope of this inner function.
nonlocal output
Next, we will push the employee root into our queue that we'll create.
queue = collections.deque([(employee)])
While the queue still has employee nodes to visit, we will continue our BFS.
while queue:
We'll start by saving the width of the queue to know how many nodes are in the next layer we are about to visit. This isn't required but it is generally helpful for BFS algorithms that calculate time and distance.
width = len(queue)
For each node within that width, we will pop an employee from the queue, append its importance to the output and then add any subordinates it has to the queue to be visited within the next layer.
for _ in range(width):
employee = queue.popleft()
output += importance[employee]
for subordinate in adjacency[employee]:
queue.append((subordinate))
Now that we have our helper function built, we just need to make the initial call on the given employee that was input and return the output.
bfs(id)
return output
Depth-First Search
The DFS solution for this is the same. We just need to swap out the helper function and substitute the queue for a call stack.
def dfs(employee:int) -> None:
nonlocal output
output += importance[employee]
for subordinate in adjacency[employee]:
dfs(subordinate)