Problem Description
Given the root of a binary tree, flatten the tree into a "linked list":
- The "linked list" should use the same
TreeNodeclass where therightchild pointer points to the next node in the list and theleftchild pointer is alwaysnull. - The "linked list" should be in the same order as a pre-order traversal of the binary tree.
Example 1:
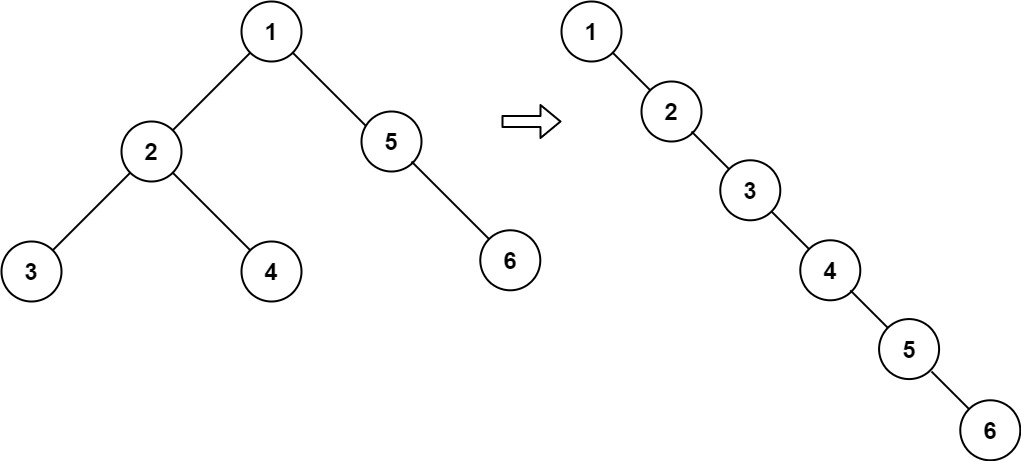
Input: root = [1,2,5,3,4,null,6] Output: [1,null,2,null,3,null,4,null,5,null,6]
Example 2:
Input: root = [] Output: []
Example 3:
Input: root = [0] Output: [0]
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -100 <= Node.val <= 100
Follow up: Can you flatten the tree in-place (with O(1) extra space)?
The description was taken from https://leetcode.com/problems/flatten-binary-tree-to-linked-list/.
Problem Solution
#Recursive DFS#O(N) Time, O(N) Space
class Solution:
def flatten(self, root: Optional[TreeNode]) -> None:
"""
Do not return anything, modify root in-place instead.
""" def postorder(node:TreeNode) -> TreeNode:
if not node:
return None
if not node.left and not node.right:
return node
left_list = postorder(node.left)
right_list = postorder(node.right)
if left_list:
left_list.right = node.right
node.right = node.left
node.left = None
if right_list:
return right_list
else:
return left_list
postorder(root)#Morris Traversal#O(N) Time, O(1) Space
class Solution:
def flatten(self, root: TreeNode) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:
return None
node = root while node:
if node.left:
tail = node.left
while tail.right:
tail = tail.right
tail.right = node.right
node.right = node.left
node.left = None
node = node.rightProblem Explanation
Recursive Depth-First Search
To solve this problem, our first thought may be to start at the bottom of the tree and change each left child node to the right child, then change the right pointer to the left child and set the left child to null.
node.left.right = node.right
node.right = node.left
node.left = NoneIn order to make these attachments correctly, the code won't be too different from what was written previously.
The main difference is we will be returning each leaf node we come across and not the head node of each current subtree and the attachments we will be making is the attachment of the right node to what was returned from the left recursive call, the rightmost leaf of the left list. The leaf nodes, the right one specifically if it exists otherwise the left one, will be the tails that we will be needing to connect. By doing this, we will be able to travel down the tree and build these lists from the bottom of the tree moving upward.
Let's create our postorder Depth-First Search function.
It will take a tree node to be visited and will return a leaf node.
def postorder(node:TreeNode) -> TreeNode:
If the current node is not null, then we have no leaf nodes to return.
if not node:
return None
if not node.left and not node.right:
return node
Otherwise, we will continue the DFS on our left and right children.
left_list = postorder(node.left)
right_list = postorder(node.right)
If the left child's recursive call returned a leaf node tail then we will attach the current right node to that left tail, set the current left head to the right child, and then set the left child to null.
This makes the previous right pointer the new leaf tail node of this left list.
if left_list:
left_list.right = node.right
node.right = node.left
node.left = None
But remember, that may not always be the case because everything we just did for the left list we also did for each left list of the previous right node's children that we just attached. This means that if we attached the right node to the end of this current left list, then the leaf node of the right node's list is our new tail.
If we have a right list, then we will return it so that our parent node knows where to attach its right node to.
Otherwise, this right node that we just attached to our left list's tail is the new leaf node tail so we will return our left list.
if right_list:
return right_list
else:
return left_list
Now that our helper function is built, we just need to make the first call on the root.
postorder(root)
Morris Tree Traversal
To tackle the follow-up question, we can also solve this by utilizing a Morris Tree Traversal.
In the previous approach, we built the tree lists from the bottom up through a postorder traversal. If we are not using any additional storage then we are going to have to build the lists from the top down because otherwise, we aren't going to be able to know which node we just came from given how large the tree can be.
We'll first check if the root is null, if that's the case then we're done because we have nothing to flatten.
if not root:
return None
Otherwise, what we can do is create an upper-level node pointer at the root.
node = root
While the root isn't null, meaning we haven't gone past the rightmost node of the tree list which will be the tail of the final list when we're finished, we will continue to rewire connections.
while node:
From there, we will check if the node has a left child list that we need to flatten.
if node.left:
If we do, then we will start from the head of that list and find the rightmost node.
tail = node.left
while tail.right:
tail = tail.right
After we do that, we will attach the upper-level node's right node to the tail of the current left list, as we did in the previous approach.
tail.right = node.right
node.right = node.left
node.left = None
Once we do that, we will iterate to the upper level's right node which is now at the tail of the left list we just flattened.
This will continue until we have flattened the entire list.
node = node.right