Find Eventual Safe States

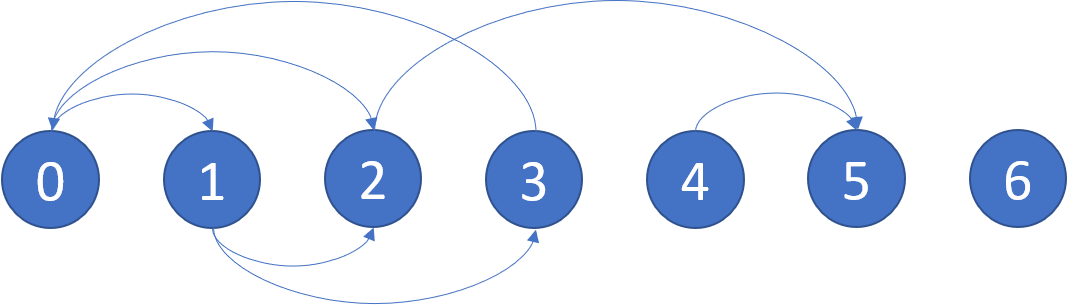
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Explanation: The given graph is shown above.
Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them.
Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6.

Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
Output: [4]
Explanation:
Only node 4 is a terminal node, and every path starting at node 4 leads to node 4.

---

We are looking for nodes that have a path to a node without any outgoing edges.

To solve this, we can start from the nodes without any outgoing edges and move backward through the path.

This type of algorithm is known as a Topological Sort.  This algorithm is good for traversing layers of nodes that either have no parents or no children, depending on the requirement.  This is done by taking an initial group of leaf nodes, visiting them first, and then collecting the next layer by removing the previous group from their respective neighbors' adjacency lists.  If after removing the nodes their neighbors now have no children, they are grouped to be visited within the next layer.

The leaf nodes that we create by traveling backward from the terminal nodes and removing each next node within the path to it will be the safe states that we will be returning.

---

Let's start by saving the number of nodes we have so that we don't have to keep writing the length later.

        n = len(graph)

 

Next, we will initialize two HashMaps.

One will be an adjacency list that maps each node to its neighbors that its pointing at.

The other will be another adjacency list but to create a mapping of nodes that are pointing at each current node.  This way, we don't have to traverse the entire adjacency list to find what nodes were pointing at each leaf node after we trim it.

This makes it slightly more difficult to implement a Topological Sort where we are looking for leaf nodes with no outgoing edges instead of incoming edges because, for incoming edges, we can just keep a count to check for leaf nodes.  Here, we will need to create an actual mapping.

        adjacency, out_edges = {}, {}
        queue = collections.deque()

 

For each node, we will initialize their place in the adjacency and outgoing edges lists with a set so that we can perform constant time deletions when trimming the leaf nodes.

        for node in range(n):
            adjacency[node] = set()
            out_edges[node] = set()

 

Next, we will traverse the graph through an enumeration.

An enumeration is a traversal through the values in the matrix with a counter that will allow us to keep track of the node.

        for node, neighbors in enumerate(graph):

 

If the current node has an empty list of neighbors, it is a terminal leaf node so we will append it to the queue and visit this layer of nodes first.

            if not neighbors:
                queue.append(node)
                continue

 

Otherwise, for each neighbor in the neighbors' list for the current node, we will add the neighbor to the node's adjacency list and add the node to the neighbor's adjacency list.

            for neighbor in neighbors:
                adjacency[node].add(neighbor)
                out_edges[neighbor].add(node)

---

Once have gathered our initial group of leaf nodes, we will begin our Breadth-First Search.

        def bfs() -> list:

 

Let's initialize our dictionary of safe nodes that we visit and the output list that we will place these nodes into.

Since the nodes need to be returned in sorted order, traversing the range of nodes and appending the ones that are in the safe dictionary will allow us to not have to sort the output list and ruin our linear time complexity.

            safe, output = {}, []

 

While we still have leaf nodes in our queue, we will continue our search.

            while queue:

 

We'll start each iteration by saving the width of the queue to know how many nodes are in the current layer.

                width = len(queue)

 

Then, for each node within that layer, we will pop it from the queue and mark it as safe.

                for _ in range(width):
                    node = queue.popleft()
                    safe[node] = True

 

For each neighbor that is pointing at the current node, we will remove the current node from their adjacency lists.  If a neighbor now has no nodes that it is pointing at, then it is a leaf node so we will visit it within the next layer.

                    for neighbor in out_edges[node]:
                        adjacency[neighbor].remove(node)
                        if not adjacency[neighbor]:
                            queue.append(neighbor)

 

After we are done visiting safe states, we will traverse the range of nodes and see if they are on the list of safe states.  If they are, we will append them to the output.

            for node in range(n):
                if node in safe:
                    output.append(node)

 

Once we have gathered all of the safe states, we will return the output.

            return output

---

Now that our helper function is built, we just need to make the initial call to return the list of safe states.

        return bfs()

---