Sum Root to Leaf Numbers

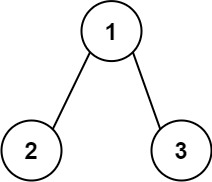
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

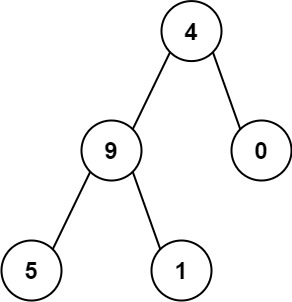
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

---

Backtracking 

If a problem requires returning every combination of something, that is usually an indication that backtracking can be implemented.  Backtracking is a Depth-First Search algorithm where if a path doesn't lead to a valid solution, or it did and now needs to travel to a different solution, the last placement is reverted from the path so that a new placement can be circulated in.

Here, we can append each number along every root-to-leaf path to a list, then once a leaf or null node is hit, we will backtrack by popping every number off the list from the current path so that numbers from each additional path can be circulated in.

Once we have each valid path combination, we will just need to traverse the list of these and sum them together.

---

Let's start by creating a paths matrix to contain each valid path we come across.

We will also need an output number which will be the sum of each of these paths.

        paths = []
        output = 0

---

Next, we will make our preorder DFS function.  

It will take a tree node to be visited and a current path list as arguments.

        def preorder(node:TreeNode, path:list) -> None:

 

Backtracking functions usually have two base cases, a good and a bad.

Our bad base case will be if we hit a root node then we have exhausted a path and will return.

            if not node:
                return

 

Our good base case will be if we have no left or right children at the current node, then we have reached a leaf node.

            if not node.left and not node.right:

 

If this is the case, we will append the current node value to the current path then append the path to the paths array and return.

Here we are converting the node values to strings when we append them to the path just because it requires fewer steps to convert a list of strings to a number than a list of numbers in Python.  This is just a shortcut for us.

            if not node.left and not node.right:
                paths.append(path + [str(node.val)])
                return

 

If we are not at a leaf node, we will append the current node to the current path and continue the DFS on our left and right children.

            path.append(str(node.val))
            preorder(node.left, path)
            preorder(node.right, path)

 

Once the DFS yoyo has returned to the current function call, we will pop off the node value from the path.

If we don't do this, then node values will remain in the path as nodes higher in the tree are visited, resulting in an incorrect sum.

            path.pop()

---

Now that our helper function is built, we need to make an initial call on the root with an empty path.

        preorder(root, [])

 

For each path in the paths list, we will join the path to a string, convert that string into a number, then increment the output by that number.

        for path in paths:
            output += int("".join(path))

 

When we have finished with that, we will return the output.

        return output

---

---

Math 

Similar to some of the problems that require adding numbers in the form of strings, linked lists, etc., we can traverse digits of a number and join those digits together by multiplying the current number by ten to create a placeholder zero that the next digit will go into.

The idea is the same as the previous solution but here we won't have arrays that we need to convert into numbers and since we don't have external storage, we won't need to backtrack.