Problem Description
Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
Example 1:
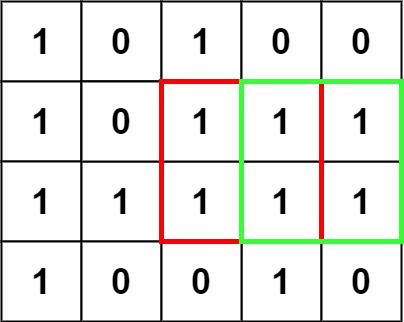
Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]] Output: 4
Example 2:

Input: matrix = [["0","1"],["1","0"]] Output: 1
Example 3:
Input: matrix = [["0"]] Output: 0
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]is'0'or'1'.
The description was taken from https://leetcode.com/problems/maximal-square/.
Problem Solution
#O(M*N) Time, O(M*N) Space
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
m, n = len(matrix), len(matrix[0])
dp = [[0] * (n+1) for row in range(m+1)]
max_side = 0
for row in range(1,m+1):
for col in range(1,n+1):
if matrix[row-1][col-1] == "1":
dp[row][col] = min(dp[row][col-1], dp[row-1][col], dp[row-1][col-1]) + 1
max_side = max(max_side, dp[row][col])
return max_side * max_sideProblem Explanation
If the problem asked for the greatest island, we'd be able to solve this with a Depth-First Search.
The problem with a square is we could calculate the greatest four sides of the square but it would be possible that there would be zeros within the boundaries that would nullify it which we wouldn't be able to easily track if we did a traditional search.
To solve this, we are going to have to continuously track the greatest square length up to each current cell, this is a Dynamic Programming method.
By tracking the greatest square length up until each current cell, if we come across a one, we'll be able to just look for the smallest square length from each top, top-left, and left neighbors, since a square has to have an even length of sides, its area will be dependent on the smallest side.
If for example, we have this square in the matrix:
| 1 | 0 |
| 1 | 1 |
The minimum side is one, so we wouldn't be able to form a square from that greater than an area of one.
If we had this square:
| 1 | 1 |
| 1 | 1 |
The minimum side is two, so we would be able to make a square with an area of four.
Once we finish traversing the matrix, we'll return our maximum, minimum side multiplied by itself to find the maximum area square that exists within the matrix.
Let's start by saving the length and width of the matrix to variables m, and n, so that we don't have to keep rewriting these later.
m, n = len(matrix), len(matrix[0])
Next, we will make our dp table that will hold the greatest square side length up to each index, equal to the size of the input matrix.
We'll have an extra row and column of zeros though since we are looking at the top, top-left, and left neighbors for each cell, this will allow us to not get an index out of bounds error when we are on the top or left borders of the matrix.
dp = [[0] * (n+1) for row in range(m+1)]
We'll also want to keep track of the maximum side outside of the dp table so that we don't have to traverse the matrix twice.
max_side = 0
After, we'll traverse the matrix.
for row in range(1,m+1):
for col in range(1,n+1):
If the current cell in the matrix is one, we may have a square.
if matrix[row-1][col-1] == "1":
To check, we'll look at the left, top, and top-left neighbor cells within the dp table. We'll take the minimum between the three and add one to it since all four of a square's sides are dependent on the smallest side we found for it.
After we mark the current cell of the maximum side up until this point within the dp table, we'll compare that current value with the maximum we have saved so far, updating it if greater.
By doing this, each time we find all four sides of an increasing square, we will have its maximum side saved within the bottom-right corner of it within our dp cache.
dp[row][col] = min(dp[row][col-1], dp[row-1][col], dp[row-1][col-1]) + 1
max_side = max(max_side, dp[row][col])
When we have finished our traversal, we will calculate the area of our maximal square by calculating the maximum, minimum side by itself.
return max_side * max_side
Additional Notes
Since we are only looking at only the previous row of our dp cache, we only need an array to save previous maximum square side values.
If we are only using an array, the only temporary variable we will need to keep track of is the top-left neighbor.
The left neighbor we can get from the previous index in the matrix. Each time we get to a new cell, if we haven't overwritten its value yet, we will be looking at the "top" cell from the previous row iteration. It is only the top-left that will need to be saved because it will be overwritten by the left cell.
To account for this, each time we are done with the top cell and have overwritten the current cell, we will iterate the top cell to be the top-left cell, because similar to how the top cell is each cell that has not yet been overwritten from the previous row iteration, the top-left cell will be that same top cell, but for the previous column iteration.
#O(M*N) Time, O(N) Spaceclass Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
m, n = len(matrix), len(matrix[0])
dp = [0] * (n+1)
max_side, top_left = 0, 0
for row in range(1,m+1):
for col in range(1,n+1):
top = dp[col]
left = dp[col-1]
if matrix[row-1][col-1] == "1":
dp[col] = min(left, top_left, top) + 1
max_side = max(max_side, dp[col])
else:
dp[col] = 0
top_left = top
return max_side * max_side