Problem Description
You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.
In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.
Return the minimum number of moves required to make every node have exactly one coin.
Example 1:
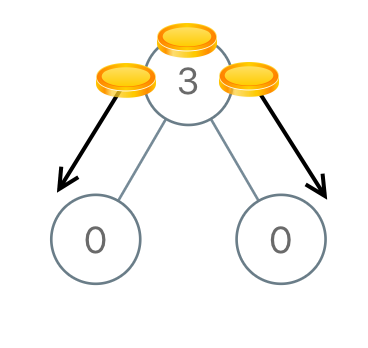
Input: root = [3,0,0] Output: 2 Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.
Example 2:
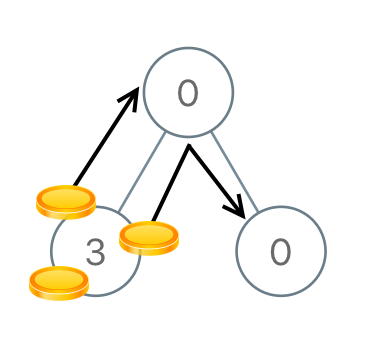
Input: root = [0,3,0] Output: 3 Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.
Example 3:
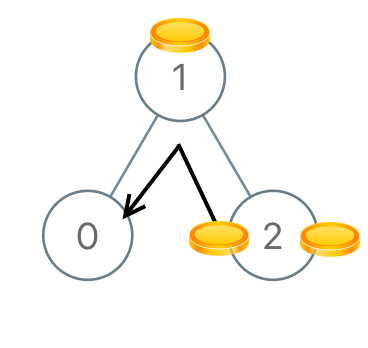
Input: root = [1,0,2] Output: 2
Example 4:
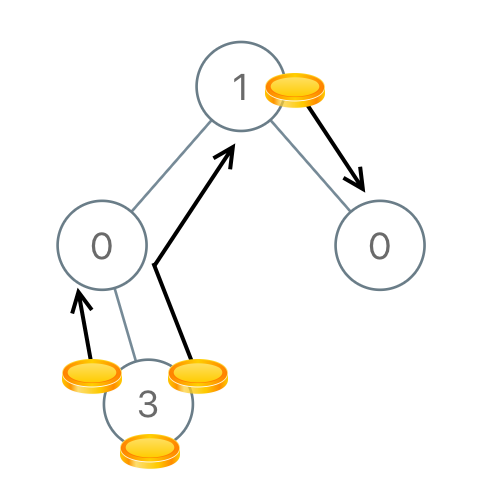
Input: root = [1,0,0,null,3] Output: 4
Constraints:
- The number of nodes in the tree is
n. 1 <= n <= 1000 <= Node.val <= n- The sum of all
Node.valisn.
The description was taken from https://leetcode.com/problems/distribute-coins-in-binary-tree/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def distributeCoins(self, root: Optional[TreeNode]) -> int:
output = 0
def postorder(node:TreeNode) -> int:
nonlocal output
if not node:
return 0
left = postorder(node.left)
right = postorder(node.right)
output += abs(left) + abs(right)
return node.val + left + right - 1
postorder(root)
return output Problem Explanation
This solution is going to be confusing if we picture the coin allocation going multiple ways like it is in the diagram.
For tree questions, a useful question to ask is "whose information do we need first?". If a node has extra coins and we'd like to allocate those coins to its children, we'll need to know how many coins we need to give to the children. On the other side of that coin, if a node needs a coin, we'll need to know if a child node has an extra one to give.
Overall, the way this solution works is coin orders begin at the bottom of the tree and are brought up to the root.
At each node, we'll increment the output by the number of absolute coin orders that were given by the current left and right children, because whether that sum is a negative two or positive two, that is still a coin that needs to be moved around from one node to another within the current branch.
At the end of the iteration, we'll add the non-absolute values to the current node value and subtract a one for this. At the base case of a zero leaf node, this will create a coin order of one, saying the current node needs a coin. If the current node value is one, then this will nullify the order because the node already has a coin. If The current node is greater than one, then this will create a coin order to give the coin surplus to the upper branch. By the time the traversal hits the root, the root will either settle its children's debts if it has all the money, or it will get money from its children.
What may make the problem confusing to visualize is the diagram showing the traversal going many directions, but it's just going up to the root always. It's either going to create a rolling coin surplus that is settled at the root or a rolling coin debt that is also settled at the root.
Let's start by creating the output counter for the minimum number of moves required to make every node have exactly one coin.
output = 0
Next, we'll make our postorder Depth-First Search helper function.
def postorder(node:TreeNode) -> int:
We'll need to first let Python know that the output counter is nonlocal to the current function and its scope exists within the outer function.
nonlocal output
Let's set a base case.
If we hit a null node, then we have zero coins to allocate to this null node. If that is the case, we will return a zero.
if not node:
return 0
Otherwise, we'll continue down the left and right branches of the tree before we begin processing any nodes.
left = postorder(node.left)
right = postorder(node.right)
Once the DFS yoyo has returned to the current node, we'll increment our output by the total number of orders needed for our left and right branches.
These nonabsolute values are either going to be positive, negative, or zero.
If a child's value is zero, then there are no coins needed to be moved to any nodes within that child's branch, if it is negative, then there are coins needed to be moved to a node within that child's branch, and if they are positive, then there are coins that are needed to be moved away from that child's branch.
Whether they are negative or positive, these are coins that need to be moved.
output += abs(left) + abs(right)
Lastly, we'll return the current node's value plus the left and right orders, minus one.
As mentioned in the beginning, this may be a consolidation of coins at some subtree roots, but it will be a consolidation at the root of the tree.
If for example, we have this subtree:
We would have two coins that need to be given to the left branch and two coins that need to be taken to the right branch. We'll add the node value, one, the left branch's return value, negative two, the right branch's value, two, and add them together then subtract one.
That will result in zero, so we'll be able to tell this subtree's parent node that there are no debts or surpluses here, otherwise, those would be passed up to be settled higher up the tree.
That is also why it is important that we incremented the output with these values prior to settling the debt because we wouldn't have been able to track how many coins were moved otherwise.
Since we are settling these debts immediately at each subtree root when are able, that ensures that we are performing these allocations in the minimum steps possible.
return node.val + left + right - 1
Now that our helper function is created, we just need to make the initial call on the root and return the output.
postorder(root)
return output