Problem Description
For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.
Example 1:
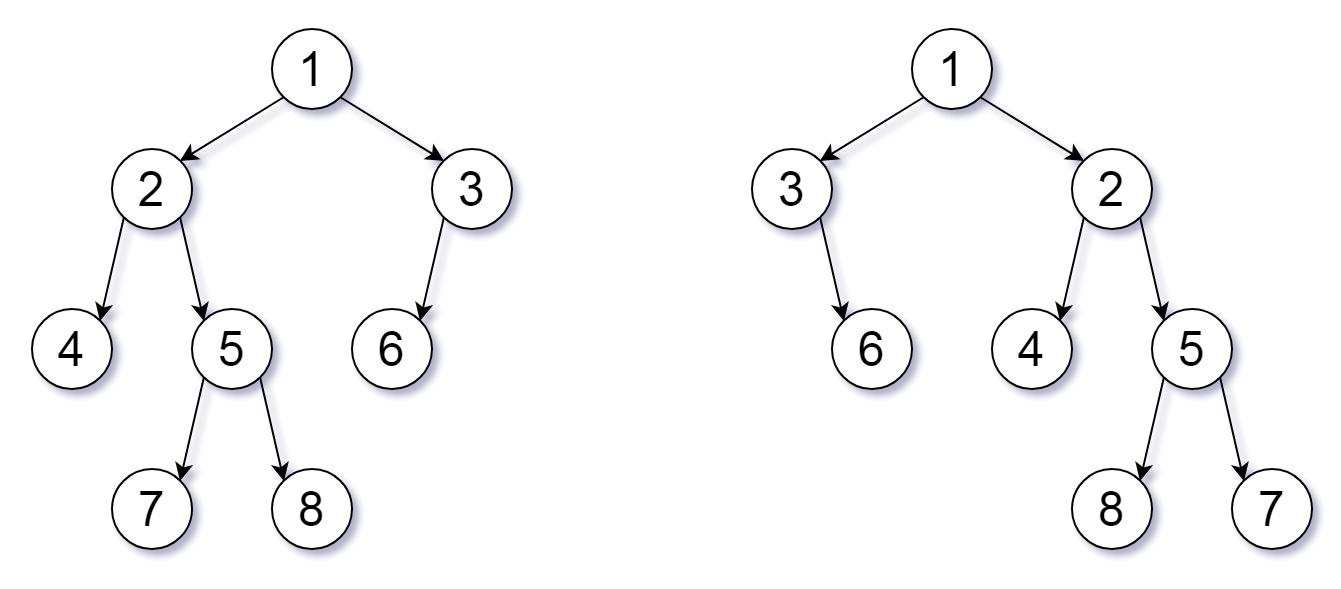
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7] Output: true Explanation: We flipped at nodes with values 1, 3, and 5.
Example 2:
Input: root1 = [], root2 = [] Output: true
Example 3:
Input: root1 = [], root2 = [1] Output: false
Example 4:
Input: root1 = [0,null,1], root2 = [] Output: false
Example 5:
Input: root1 = [0,null,1], root2 = [0,1] Output: true
Constraints:
- The number of nodes in each tree is in the range
[0, 100]. - Each tree will have unique node values in the range
[0, 99].
The description was taken from https://leetcode.com/problems/flip-equivalent-binary-trees/.
Problem Solution
#O(M+N) Time, O(M+N) Space
class Solution:
def flipEquiv(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool:
if root1 == root2:
return True
if not root1 or not root2:
return False
def preorder(node:TreeNode, tree:dict) -> None:
if not node:
return
if node.val not in tree:
tree[node.val] = []
if node.left:
tree[node.val].append(node.left.val)
preorder(node.left, tree)
if node.right:
tree[node.val].append(node.right.val)
preorder(node.right, tree)
tree_one, tree_two = {}, {}
preorder(root1, tree_one)
preorder(root2, tree_two)
for node in tree_one:
if node not in tree_two:
return False
if tree_one[node] != tree_two[node] and \
tree_one[node] != tree_two[node][::-1]:
return TrueProblem Explanation
The shortest solution to this problem is to have a recursive function where we would check if two nodes are equal, then check if their two child nodes are equal as is, or that they are equal when the left and right pointers are swapped.
A longer, but maybe more intuitive approach is to utilize a HashMap to distinguish a mapping between each node and their children within both trees.
We can perform a preorder traversal on both trees and map each child node value to each parent. Then, we can traverse the hashmaps and see if the node's children are equal or equal when reversed within both trees.
First off, let's take care of null test cases.
If both trees are equal, then we can return true because they are already equivalent.
if root1 == root2:
return True
If one node is null while the other isn't, then we will return false because we couldn't swap either one to get the other.
if not root1 or not root2:
return False
Otherwise, let's start by creating our preorder Depth-First Search helper function that we will use to map each child to their parent.
The function will take a node to be visited and a dictionary to place the node into.
def preorder(node:TreeNode, tree:dict) -> None:
We don't actually need to set a base case here because we are going to be recursing non-null children and we just checked that the root isn't null, but let's just do it anyway for good practice.
If we hit a null node, we will return.
if not node:
return
Otherwise, if the node value isn't already initialized in our HashMap, which shouldn't be because we are using unique values, we will initialize it with a list value.
if node.val not in tree:
tree[node.val] = []
Next, if we have a left or right child then we will append their values to the node's key and continue our DFS on them next.
if node.left:
tree[node.val].append(node.left.val)
preorder(node.left, tree)
if node.right:
tree[node.val].append(node.right.val)
preorder(node.right, tree)
Now that our helper function is built, let's initialize two empty dictionaries, one for each tree, then call the preorder function on both roots with these two respective dictionaries.
tree_one, tree_two = {}, {} preorder(root1, tree_one)
preorder(root2, tree_two)
Lastly, we will traverse each node in the first tree dictionary.
for node in tree_one:
If the node isn't in the second dictionary, then there's no way we could flip this tree to become equivalent to the other.
If this is the case, we will return false.
if node not in tree_two:
return False
Otherwise, we will check if the children of this node in both dictionaries are the same, or that they are the same when reversed.
If neither of these is true, we will return false.
if tree_one[node] != tree_two[node] and \
tree_one[node] != tree_two[node][::-1]:
If we were able to cross-reference each node's children are equal or can be flipped to be equal, we will return true.
return True