Problem Description
Given the root of a binary tree, each node in the tree has a distinct value.
After deleting all nodes with a value in to_delete, we are left with a forest (a disjoint union of trees).
Return the roots of the trees in the remaining forest. You may return the result in any order.
Example 1:
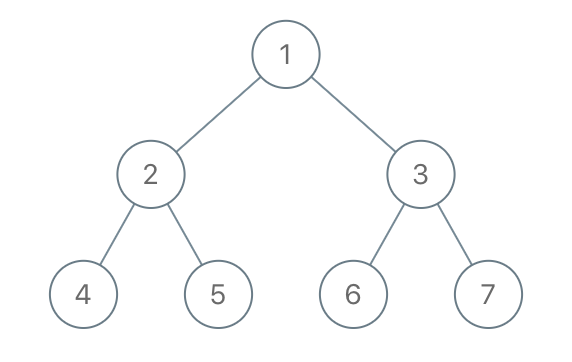
Input: root = [1,2,3,4,5,6,7], to_delete = [3,5] Output: [[1,2,null,4],[6],[7]]
Example 2:
Input: root = [1,2,4,null,3], to_delete = [3] Output: [[1,2,4]]
Constraints:
- The number of nodes in the given tree is at most
1000. - Each node has a distinct value between
1and1000. to_delete.length <= 1000to_deletecontains distinct values between1and1000.
The description was taken from https://leetcode.com/problems/delete-nodes-and-return-forest/.
Problem Solution
#DFS
#O(N) Time, O(N) Space
class Solution:
def delNodes(self, root: TreeNode, to_delete: List[int]) -> List[TreeNode]:
to_delete_set = set(to_delete)
output = []
def dfs(node:TreeNode, parent:TreeNode, child:str) -> None:
if not node:
return
if not parent and node.val not in to_delete_set:
output.append(node)
if node.val in to_delete_set:
if child == "L":
parent.left = None
if child == "R":
parent.right = None
dfs(node.left, None, None)
dfs(node.right, None, None)
else:
dfs(node.left, node, "L")
dfs(node.right, node, "R")
dfs(root, None, None)
return output#BFS
#O(N) Time, O(N) Space
class Solution:
def delNodes(self, root: TreeNode, to_delete: List[int]) -> List[TreeNode]:
to_delete_set = set(to_delete)
output = []
def bfs(root:TreeNode, parent:TreeNode, child:str) -> None:
if not root:
return
queue = collections.deque([(root, parent, child)])
while queue:
node, parent, child = queue.popleft()
if not parent and node.val not in to_delete_set:
output.append(node)
if node.val in to_delete_set:
if child == "L":
parent.left = None
if child == "R":
parent.right = None
if node.left:
queue.append((node.left, None, None))
if node.right:
queue.append((node.right, None, None))
else:
if node.left:
queue.append((node.left, node, "L"))
if node.right:
queue.append((node.right, node, "R"))
bfs(root, None, None)
return outputProblem Explanation
Depth-First Search
There are several ways to solve this problem.
The most intuitive way may be a preorder DFS traversal.
During the traversal, we will keep track of the parent node for each current node. If we find that the current node is in the list of nodes to be deleted, we can reference its parent node then set the parent node's respective child to null.
By doing that, when we traverse the deleted node's children, we will just need to check if the parent node is null to know whether the current node is a new root of its subtree.
If we picture each branch of the tree as a bridge, this would be similar to us breaking the bridge after we have already crossed it from the preorder traversal.
Let's start off by pushing the list of nodes to delete into a set.
Since we can have up to a thousand nodes in this list, having to traverse the entire list for each node to see if it should be deleted will take a long time.
We'll also initialize our output list of nodes that are the roots of their subtrees after deleting their parents.
to_delete_set = set(to_delete)
output = []
Next, we will create our DFS function.
Each function call will require a node to be visited, a parent node of that node, and a child identifier which will tell us whether the node is a left child or a right child.
def dfs(node:TreeNode, parent:TreeNode, child:str) -> None:
The base case will be if we hit a null node, then we have exhausted a DFS branch and will begin moving back up.
if not node:
return
Otherwise, we will first check if the current node has no parent and its value isn't in the list of nodes to be deleted.
If it has no parent, then that means it is a root of its subtree now, but that is only if we don't need to delete this node as well.
If both of these cases are true, then we will append it to the output.
if not parent and node.val not in to_delete_set:
output.append(node)
Otherwise, if the node value needs to be deleted then we will refer to the appropriate identifier for which child node it is, and then set that child node of the parent to null
if node.val in to_delete_set:
if child == "L":
parent.left = None
if child == "R":
parent.right = None
Once we have done that, we will visit the child nodes next but specify in the function call that this node has no parent so it gets set as a subtree root if it doesn't also need to be deleted.
For the scenario that a child node of this node does need to be deleted, however, we will also set the child node identifier to null too. This way, we don't try to access a null value's left or right children.
dfs(node.left, None, None)
dfs(node.right, None, None)
If we aren't deleting the current node, we will visit each child node, set the current node as their parent, and set "L" or "R" as their identifier.
else:
dfs(node.left, node, "L")
dfs(node.right, node, "R")
Now that our DFS helper function is created, we just need to make the initial call on the root, set its parent to null, and its child identifier to null since it has no parent.
dfs(root, None, None)
return output
Breadth-First Search
Since we did a preorder traversal, switching to a BFS implementation is quite simple.
If we want to switch from a preorder traversal to a BFS, and this works almost every time, we just need to swap out the function arguments for a tuple with the same parameters, swap the call stack out for a queue, and create a while loop that will run while the queue isn't empty.
def bfs(root:TreeNode, parent:TreeNode, child:str) -> None: if not root: return queue = collections.deque([(root, parent, child)]) while queue: node, parent, child = queue.popleft() if not parent and node.val not in to_delete_set: output.append(node) if node.val in to_delete_set: if child == "L": parent.left = None if child == "R": parent.right = None if node.left: queue.append((node.left, None, None)) if node.right: queue.append((node.right, None, None)) else: if node.left: queue.append((node.left, node, "L")) if node.right: queue.append((node.right, node, "R"))