Problem Description
Given the root of a binary tree, return the leftmost value in the last row of the tree.
Example 1:
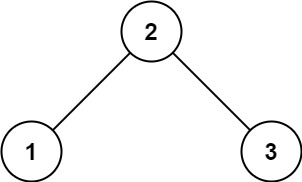
Input: root = [2,1,3] Output: 1
Example 2:
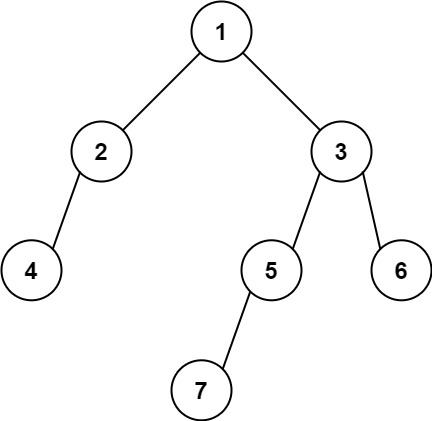
Input: root = [1,2,3,4,null,5,6,null,null,7] Output: 7
Constraints:
- The number of nodes in the tree is in the range
[1, 10^4]. -2^31 <= Node.val <= 2^31 - 1
The description was taken from https://leetcode.com/problems/find-bottom-left-tree-value/.
Problem Solution
#BFS
#O(N) Time, O(N) Space
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
def bfs() -> int:
leftmost = None
queue = collections.deque([(root)])
while queue:
width = len(queue)
leftmost = None
for _ in range(width):
node = queue.popleft()
if leftmost == None:
leftmost = node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return leftmost
return bfs()#DFS
#O(N) Time, O(N) Space
class Solution:
def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
output = []
def dfs(node: TreeNode, level: int) -> None:
if not root:
return
if level == len(output):
output.append(node.val)
if node.left:
dfs(node.left, level + 1)
if node.right:
dfs(node.right, level + 1)
dfs(root, 0)
return output[-1]Problem Explanation
Breadth-First Search
The BFS solution to this problem is fairly straightforward.
We can run a level-order traversal on the tree with a leftmost variable.
We will set this variable to the first node within each level so that after we finish searching the last level of the tree, we can return the leftmost value from the bottom level.
Let's start by creating our BFS function.
def bfs() -> int:
We will create a variable to keep track of the leftmost node of each level and also our queue, which will be initialized with the root node.
leftmost = None
queue = collections.deque([(root)])
Our BFS will continue while there are still nodes in the queue.
while queue:
We will start each iteration by getting a count of the next layer we are about to traverse and also by setting the leftmost value to none.
width = len(queue)
leftmost = None
Then, for each node within the current layer, we will pop it from the queue and check if the leftmost variable hasn't been set yet.
If it has, then we will set it to the first node in the level.
for _ in range(width):
node = queue.popleft()
if leftmost == None:
leftmost = node.val
Then, we will append any children nodes to the next layer to be searched.
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
Once we have traversed the entire tree, we will return the last leftmost variable that we set.
return leftmost
After our BFS helper function has been created, we just need to make the initial call to return the bottom leftmost value.
return bfs()
Depth-First Search
The DFS solution is a little trickier in theory but easier to implement.
The basic idea is we will only have one leftmost node per level. From that requirement, we can use the length of the output as an indicator for whether or not the leftmost node has been picked yet for the given level.
We'll run the preorder DFS on the left child first of each node so that we favor the left side of the tree in our search. If the length of the output is the same as the level, then that means we haven't chosen a leftmost node from the current level yet so we can append the first node seen in our search since the DFS path will go to the farthest path down the left side of the tree before moving toward any right paths.
Once we have traversed the entire tree, the leftmost node at the bottom of the tree will be the last index of the output.
Let's start by initializing our output array.
output = []
Next, we will create our recursive dfs function.
The function will take a level integer so that we can keep track of the level each node is on, and it will also take the node it is being called on.
def dfs(node: TreeNode, level: int) -> None:
If the current node is null, we have reached the end of a valid path so we will return.
if not root:
return
Otherwise, we will check if the length of the output is the same as the level value.
For example, if the length of the output is zero and we are on level zero, the root level, we know that we haven't picked a node from this level yet so we will pick the first node we see in our DFS.
Notice we put the base case before the function calls in the function. This ensures that the DFS is picking values as it moves down the search.
if level == len(output):
output.append(node.val)
After appending a value or not, we will continue the DFS on the left node first then the right while incrementing the level value by one.
if node.left:
dfs(node.left, level + 1)
if node.right:
dfs(node.right, level + 1)
Now that our helper DFS function is made, we just need to make the initial call on the root at level zero.
Once we have picked the leftmost node of each level, we will return the last one we picked.
dfs(root, 0)
return output[-1]