Max Increase to Keep City Skyline

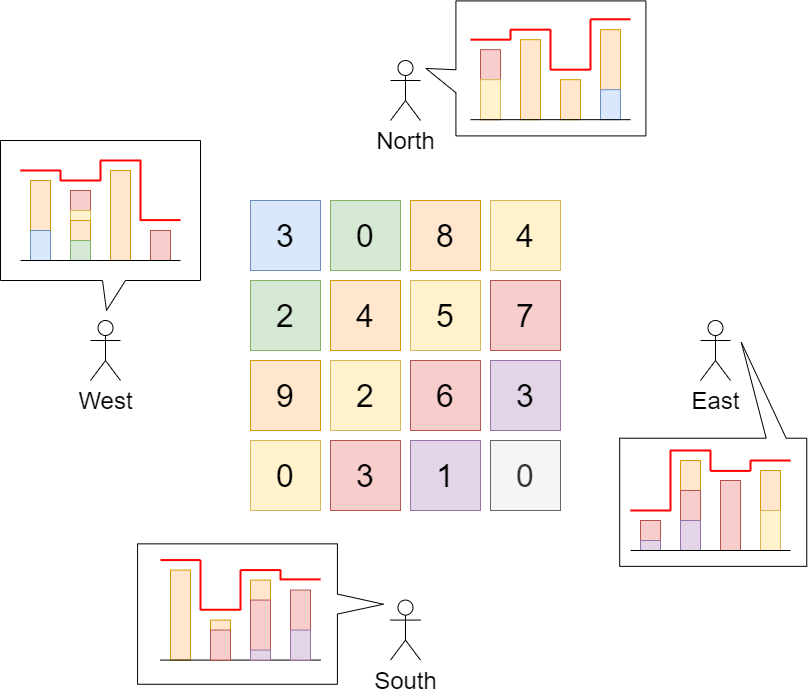
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
            [7, 4, 7, 7],
            [9, 4, 8, 7],
            [3, 3, 3, 3] ]

Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: Increasing the height of any building will result in the skyline changing.

---

The problem states that we can't increase a building that would obstruct the contour of the skyline from any cardinal direction.

Let's go ahead and draw out what the skylines would look like from the north and east view, using the first example.

From the north we would see:

3	0	8	4
	4		7
9

 

From the east we would see:

		8	4
			7
9			3
	3		0

 

We may recognize a pattern now.

From each viewpoint, we would see the immediate buildings in front of us, but we would also see any larger buildings behind the immediate buildings if they are larger.

To solve this problem, we can traverse the grid once to cache the largest building within each row and column.

Then, for each building cell, we can increment the output increase size by the difference between the current building and the minimum between the largest building in the current row and the largest building in current the column.

Let's look back at the first example.

3	0	8	4
2	4	5	7
9	2	6	3
0	3	1	0

 

If we wanted to change the seventh building, with the height of five, we would only be able to increase it to the minimum between seven and eight, the largest buildings in its row and column.

3	0	8	4
2	4	5	7
9	2	6	3
0	3	1	0

 

If we made it taller than seven, then it would become newly visible from the east side, changing the contour of the skylines from that viewpoint.  If we made it taller than eight, then it would become newly visible from the north side.

That is why we can only increment a building to the minimum between the tallest building in its row and its column.

---

Let's start by saving the length and width of the grid to variables m, and n, so that we don't need to keep rewriting these later.

        m, n = len(grid), len(grid[0])

 

We'll then initialize our maximum rows and maximum columns hashmap which we will store the tallest building in each row and column.

        max_rows, max_cols = {}, {}

 

Next, we will make our running increase counter which is what we will be returning at the end.

        increase = 0

 

To make things easier for us for our first pass, let's traverse the number of rows and columns we have and initialize each row and column to negative infinity within our hashmaps.

We could skip this step and use a default dictionary instead from the collections library, but let's just play it safe and do this by hand.

        for i in range(n):
            max_rows[i] = float("-inf")
            max_cols[i] = float("-inf")

 

After, we will make our initial pass through the grid and check each building as the maximum for its row and column.

        for row in range(m):
            for col in range(n):
                max_rows[row] = max(max_rows[row], grid[row][col])
                max_cols[col] = max(max_cols[col], grid[row][col])

 

Then, we will make our second pass to increase each building by the height difference between itself and the tallest building in its row and column.

        for row in range(m):
            for col in range(n):
                increase += min(max_rows[row], max_cols[col]) - grid[row][col]

 

Once we have finished with our increase count, we will return it.

        return increase

---