Problem Description
Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.
A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.
Example 1:
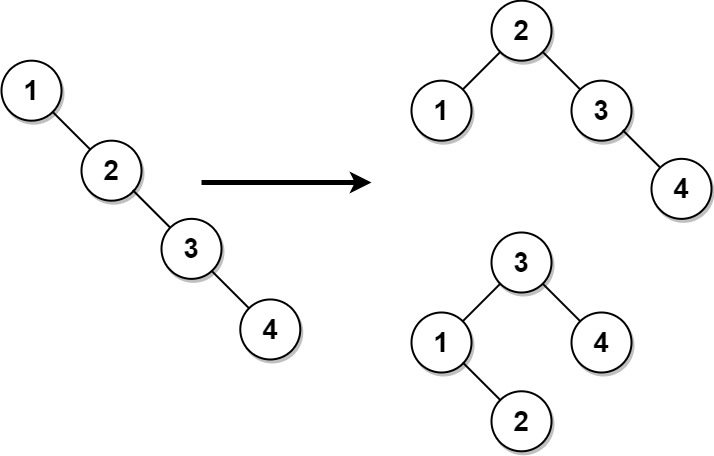
Input: root = [1,null,2,null,3,null,4,null,null] Output: [2,1,3,null,null,null,4] Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.
Example 2:
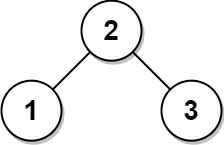
Input: root = [2,1,3] Output: [2,1,3]
Constraints:
- The number of nodes in the tree is in the range
[1, 10^4]. 1 <= Node.val <= 10^5
The description was taken from https://leetcode.com/problems/balance-a-binary-search-tree/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def balanceBST(self, root: TreeNode) -> TreeNode:
tree = []
def inorder(node: TreeNode) -> int:
if not node:
return
left = inorder(node.left)
tree.append(node.val)
right = inorder(node.right)
def construct(left:int, right:int) -> TreeNode:
if left > right:
return None
mid = (left + right) // 2
node = TreeNode(tree[mid])
node.left = construct(left, mid-1)
node.right = construct(mid+1, right)
return node
inorder(root)
return construct(0, len(tree)-1)Problem Explanation
This problem is a combination of Binary Tree Inorder Traversal and Convert Sorted Array to Binary Search Tree.
The overall idea of this question is we want to find the median node within an unbalanced tree, make that the root, and do the same thing for its left and right branches.
One thing to note here that isn't in the constraints is that it may seem that this has to be done in place, but the constraints just state the node values need to be the same, but we don't need to reorder the original tree.
To solve this, we can flatten the binary tree values into an array by performing an inorder traversal, then we can convert that flattened tree into a new tree by performing construction Depth-First Search.
Let's start by initializing our tree array.
tree = []
Next, we will make an inorder traversal helper function that will take a node, recurse its left child, append the node's value to the tree array, then recurse its right child.
Since this is a binary search tree, this will allow us to get each node in order, as the name suggests, because each left child will be smaller than its parent, and each right child will be greater than its parent.
def inorder(node: TreeNode) -> int:
if not node:
return
left = inorder(node.left)
tree.append(node.val)
right = inorder(node.right)
Next, we will create a construct function to build the tree from the flattened tree array.
We will achieve this by utilizing both left and right pointers so that we can recursively pick a middle node from each range and create a subtree root from it.
def construct(left:int, right:int) -> TreeNode:
During each call, if the left pointer is greater than the right pointer, then we have run out of elements to set a node with from the current array partition.
We will return none if this is the case and this child will be null.
if left > right:
return None
Otherwise, we will calculate the current middle value from the mean of the current call's left and right pointers.
We will then create a node using the element at the middle index.
mid = (left + right) // 2
node = TreeNode(tree[mid])
Once we have created our node, we will call the function on the left and right children.
The left child will be chosen using the array partition between the left pointer and one index to the left of the middle index.
The right child will be chosen using the partition between one index to the right of the middle index and the right pointer.
We don't include the middle element because we already have it set as a node.
node.left = construct(left, mid-1)
node.right = construct(mid+1, right)
Once values are returned from the previous function calls, we will return our current call's subtree root node.
return node
Now that we have our helper functions built, we just need to call the inorder function on the root node to flatten the tree, then from that flattened tree, we will construct a new tree with the initial range of the entire tree.
inorder(root)
return construct(0, len(tree)-1)