Spiral Matrix II

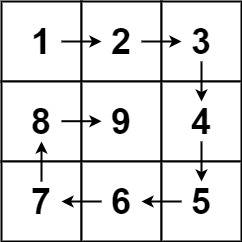
Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

Input: n = 1
Output: [[1]]

---

Traverse Perimeter

This algorithm is going to be the same as the first Spiral Matrix problem.  The only difference is we will need to create a matrix that we will traverse and have a running number that we will increment after each placement.

If we look at the picture shown in the problem description, we can see that the spiral traversal moves to the right across the top row, then to the bottom across the right column, then to the left across the bottom row, then back to the top across the left column.

What it does after is it repeats the process but within the next layer.

Noticing that, we can solve this problem by iteratively appending all elements within the outer perimeter to the matrix then pushing the perimeter inward by shrinking the top, bottom, left, and right bounds of what the next layer should be.

---

Let's start by initializing our output matrix of zeros and our initial number of one.

        matrix = [[0] * n for row in range(n)]
        num = 1

 

Next, we will define the bounds of our perimeter.

Our top pointer will be set to zero for the first array row within the matrix.  Our bottom pointer will be the length of the matrix minus one, which will give us the final row of the matrix.

Our left pointer will be set to zero for the first index of an inner matrix.  Our right pointer will be set to the length of the first array minus one, which will give us the last index we will need to travel to moving from left to right, and the first index we would need to start from moving from right to left.

        top, bottom = 0, len(matrix) -1
        left, right = 0, len(matrix[0]) -1

 

Next, let's create a loop that will run while our left pointer hasn't passed our right pointer and while our top pointer hasn't passed our bottom pointer.

Once this happens, we will have traversed the entire matrix.

        while left <= right and top <= bottom:

 

Let's begin our traversals.

First, we will traverse and append each element from the left to the right on the top side.

We'll need to add one to the right range to include it since Python excludes it from the range.

            for col in range(left, right + 1):
                matrix[top][col] = num
                num += 1

 

Next, we will traverse and append each element from the top to the bottom on the right side. 

Here, we will need to increment the top pointer by one to move it down once index since we just appended the top-right element within the previous loop.

Again, we will need to add one to the bottom index to include it since it will be excluded from the range.

            for row in range(top + 1, bottom + 1):
                matrix[row][right] = num
                num += 1

 

Next, we will traverse and append each element from the right to the left on the bottom side.

We'll need to decrement the right pointer by one to move it left one index since we just included the bottom-right element in the previous loop.

We also need to subtract one to the left index to include it within the range.

Before appending any elements, we first need to check if the top pointer has reached the bottom pointer.  If it has, then that means that our top and bottom sides of the perimeter have been squished into a single row so we will want to break from our loop.  We don't want to double append the elements from when we traversed the row from left to right.

            for col in range(right-1,left-1,-1):
                if top == bottom:
                    break
                matrix[bottom][col] = num
                num += 1

 

Last, we will traverse and append each element from the bottom to the top on the left side.

We'll need to decrement the bottom pointer by one to move it up one index since we just included the bottom-left element in the previous loop.

We also included the top-left element in the first for loop, so we will keep top as the ending index of the range since Python will stop the loop one index before it.

Also, before appending any elements, we first need to check if the left pointer has reached the right pointer.  If it has, then that means that our left and right sides of the perimeter have been squished into a single column so we will want to break from our loop.  We don't want to double append the elements from when we traversed the column from top to bottom.

            for row in range(bottom-1,top,-1):
                if left == right:
                    break
                matrix[row][left] = num
                num += 1

 

Finally, we will squish in our perimeter by moving our top pointer down, our bottom pointer up, our left pointer right, and our right pointer left.

            top += 1
            bottom -= 1
            left += 1
            right -=1

 

Once we have broken from our while loop, that means the matrix has been traversed so we will return our output array.

        return matrix

---

---

Depth-First Search

This question can also be solved with a DFS.

A DFS is useful for matrix problems because if we set up our recursive calls to visit the right neighbor, then the bottom, then the left, then the top, by default the DFS will traverse all the way to the right until it runs out of bounds, then all the way down, then all the way left, then all the way up.

The only tweak we will need to make to a normal four-neighbor matrix DFS is we will require a flag to let us know whether we are moving all the way to the top which will be explained later.

---

Same as the iterative version, let's first create our output matrix and initialize a running number to one.

        output = [[0] * n for row in range(n)]
        num = 1

---

Next, let's make a helper function to check if a coordinate is in bounds and unseen.

        def in_bounds(row:int, col:int) -> bool:

 

If the row and column coordinates are outside the bounds of our matrix, or the cell has already been seen and marked, we will return false.  

            if row < 0 or col < 0 or row >= n or col >= n:
                return False
            if output[row][col] != 0:
                return False

 

Otherwise, we will return true.

            return True

---

Let's create our recursive, DFS function next.

        def dfs(row:int, col:int, up:bool) -> None:

 

Being a recursive function, let's make sure we set a base case.

Our base case will be if we have a row or column that is not in bounds or has already been visited, we have exhausted this DFS direction path so we will return from here.

            if not in_bounds(row, col):
                return

 

Otherwise, let's make a reference to our nonlocal running number so that Python knows this integer exists outside the scope of the current DFS function.

After doing that, we will mark the current cell as the running number and increment it by one.

            nonlocal num
            output[row][col] = num
            num += 1

 

Here is the trick of the problem.

If we don't have a flag to let us know that we're going all the way up then once we get to the cell above the bottom-left corner, we will end up moving to the right instead of going all the way up.

1	2	3	4
0	0	0	5
11	12	13	6
10	9	8	7

 

To account for this, we will check if this flag is set and immediately move up if it is.

            if up:
                dfs(row-1, col, True)

 

If we are not moving up, or have finished moving up to the topmost unmarked cell on the left side of the matrix, we will continue the DFS in all four directions, setting the up flag to true when we recurse the top cell.

            dfs(row, col+1, False)
            dfs(row+1, col, False)
            dfs(row, col-1, False)
            dfs(row-1, col, True)

---

Now that we have our helper functions built, we just need to make our initial DFS call on the first row and column then return the output once the DFS has completed.

        dfs(0, 0, False)
        return output

---