Problem Description
You are given an integer length and an array updates where updates[i] = [startIdxi, endIdxi, inci].
You have an array arr of length length with all zeros, and you have some operation to apply on arr. In the ith operation, you should increment all the elements arr[startIdxi], arr[startIdxi + 1], ..., arr[endIdxi] by inci.
Return arr after applying all the updates.
Example 1:
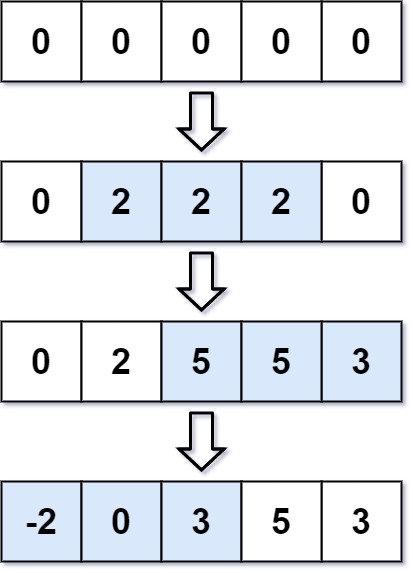
Input: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]] Output: [-2,0,3,5,3]
Example 2:
Input: length = 10, updates = [[2,4,6],[5,6,8],[1,9,-4]] Output: [0,-4,2,2,2,4,4,-4,-4,-4]
Constraints:
1 <= length <= 10^50 <= updates.length <= 10^40 <= startIdxi <= endIdxi < length-1000 <= inci <= 1000
The description was taken from https://leetcode.com/problems/range-addition/.
Problem Solution
#O(N+U) Time, O(N) Space
class Solution:
def getModifiedArray(self, length: int, updates: List[List[int]]) -> List[int]:
output = [0] * length
for start, end, inc in updates:
output[start] += inc
if end + 1 < length:
output[end+1] -= inc
for i in range(1, length):
output[i] += output[i-1]
return outputProblem Explanation
If we are given a problem that requires us to sum a sublist range multiple times, without having to revisit the same summed values, we can instead consider a Prefix Sum.
For this question, we can initialize an output array that we will build a prefix sum in, apply the given changes on the borders of the range given, and then complete the prefix sum implementation to carry each change over to their appropriate range.
Let's start by initializing an output array of the input length.
output = [0] * length
For each update, we will apply the update to the borders of the range.
for start, end, inc in updates:
We'll apply it to the starting index first.
output[start] += inc
Then, we will apply the negation of the update to the index directly after the ending index of the range.
We'll want to do this so that by the time we reach the end of the range when we're building our prefix sum, this update isn't applied to any later indices.
If there are no later indices, we don't have to worry about this.
if end + 1 < length:
output[end+1] -= inc
Once we have made the updates required, we will go through our output and build our prefix sum.
This is a cumulative sum where each index is the running sum of each index before it.
This will allow us to roll each update across each starting and ending range that we just applied.
for i in range(1, length):
output[i] += output[i-1]
Once we have our prefix sum built, we will return it.
return output