Problem Description
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any path.
Example 1:
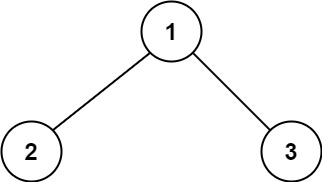
Input: root = [1,2,3] Output: 6 Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
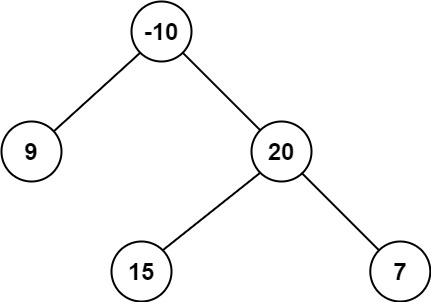
Input: root = [-10,9,20,null,null,15,7] Output: 42 Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints:
- The number of nodes in the tree is in the range
[1, 3 * 10^4]. -1000 <= Node.val <= 1000
The description was taken from https://leetcode.com/problems/binary-tree-maximum-path-sum/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def maxPathSum(self, root: Optional[TreeNode]) -> int:
max_path = -1001
def postorder(node:TreeNode) -> int:
nonlocal max_path
if not node:
return 0
left = max(postorder(node.left), 0)
right = max(postorder(node.right), 0)
path_sum = left + right + node.val
max_path = max(max_path, path_sum)
return node.val + max(left, right)
postorder(root)
return max_pathProblem Explanation
Let's clear some things up before we get into the explanation.
The description says we are looking for any path, but it fails to mention that we are supposed to look for any single path that doesn't join at a node and continue.
If we had a tree like this:
This would count as a single path because it is a path that is going through a node and not continuing from it.
Okay, now for the explanation.
The problem is like a combination of Diameter of Binary Tree and Maximum Subarray.
We are looking for a path that may or may not go through the root and will provide the maximum sum possible.
If the path may or may not go through the root, then we won't want to start our search from the root. It'd make more sense to visit it last with a postorder traversal Depth-First Search, as we did in Diameter of Binary Tree. Since the nodes can contain negative values, we can also implement a variation of Kadane's Algorithm on this, as we did in Maximum Subarray.
Let's start by initializing our maximum path to the first smallest value outside the bounds of the given node value constraints so that it will be overwritten during our traversal.
max_path = -1001
Next, we will build our recursive, postorder DFS function.
The function will take a node and will return the maximum path up to that node from its children up.
def postorder(node:TreeNode) -> int:
We'll need to clarify that this maximum path variable is located outside the scope of this inner function within each function call so that Python doesn't throw an error.
nonlocal max_path
Now let's set our base case.
If we have reached a null node, then we can begin summing node values to bring to our parent nodes.
If this is the case, we will return a zero.
if not node:
return 0
If we haven't reached a base case yet, we will continue our postorder traversal on the left and right children.
Since we can have negative values, we will want to take the maximum between what path sum they return and zero. This will make it to where we only consider positive values, like in Kadane's algorithm.
left = max(postorder(node.left), 0)
right = max(postorder(node.right), 0)
When the DFS yoyo comes back up and we have both of our child node values, we will take the path sum of if we were to join the left and right paths through the current node.
Then, we will compare that path sum to the maximum we have saved.
path_sum = left + right + node.val
max_path = max(max_path, path_sum)
Once we have done that, we will return the current node value plus the maximum single child path so that we are only considering maximum single paths within our traversal.
return node.val + max(left, right)
Now that we have our function built, we just need to make the initial call on the root and return the maximum path sum.
postorder(root)
return max_path