Path With Maximum Minimum Value

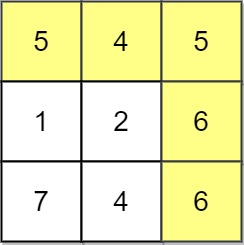
Input: grid = [[5,4,5],[1,2,6],[7,4,6]]
Output: 4
Explanation: The path with the maximum score is highlighted in yellow. 

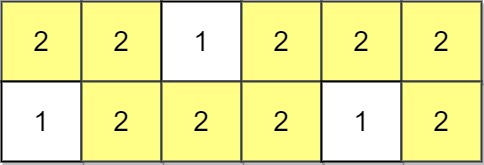
Input: grid = [[2,2,1,2,2,2],[1,2,2,2,1,2]]
Output: 2

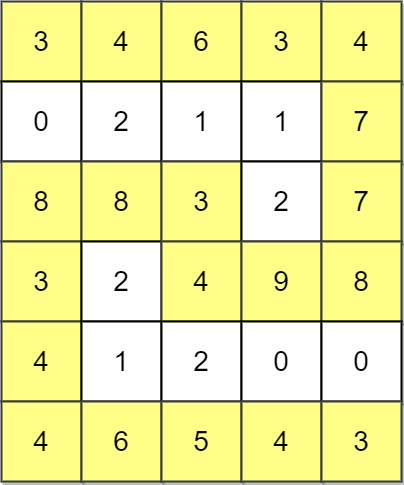
Input: grid = [[3,4,6,3,4],[0,2,1,1,7],[8,8,3,2,7],[3,2,4,9,8],[4,1,2,0,0],[4,6,5,4,3]]
Output: 3

---

This question is nearly the same as Swim in Rising Water.

If we are given a matrix and are asked to find the shortest path, that is typically an indication that Breadth-First Search will be implemented.  

However, since each cell contains a time cost to swim to their elevation, this is almost like being handed a matrix with weighted points.  We wouldn't want to explore every neighbor cell to find the shortest path, but the cells with the least time costs that we'd have to wait to swim to them which are adjacent to the current one.

To solve this, we can perform a BFS but through the implementation of a heap instead of a queue.  This will allow us to continuously pick the next cell with the shortest time cost and traverse the least costly path through the matrix.  This could be considered a variation of Dijkstra's algorithm.

---

Let's start by initializing our heap and dictionary for seen cells.

        seen, heap = {}, []

 

We'll also want to create a list of delta neighbor coordinates for the four surrounding cells of each cell.  We can utilize these values later to calculate all four neighbors of a given cell.

        neighbors = [(0,1), (1,0), (0,-1), (-1,0)]

 

Let's also want to cache the length and width of the grid so that we don't have to keep rewriting this later.

        m, n = len(grid), len(grid[0])

 

Here, we'll go ahead and make a helper function to let us know if the neighbor we are about to visit is valid.

If the row or column is outside the bounds of the array or has already been visited, the function will return false.  Otherwise, it will return true.

        def in_bounds(row:int, col:int) -> bool:
            if row < 0 or col < 0 or row >=m or col >=n:
                return False
            if (row, col) in seen:
                return False
            return True

 

Now we can begin our BFS.

We'll start with the first cell, so we will put its score, row, and column into the heap then mark the row and column as seen.

Python uses min-heaps by default, so to make a make-shift max-heap from a min-heap, we can negate each value so that the largest positive value will become the smallest value when negative.  We'll just need to make sure to negate the values whenever we push and pop them.

        heap.append((-grid[0][0],0,0))
        seen[(0,0)] = True

 

While we still have cells we need to visit in the heap, we are still traveling through the matrix.

        while heap:

 

We'll start each iteration off by popping the cell with the least time cost that we'd have to wait to swim to it.

If that cell is the last cell of the matrix, we will return the smallest score cost to travel this shortest path.

            score,row,col = heapq.heappop(heap)
            if (row, col) == (m-1, n-1):
                return -score

 

Otherwise, we will look at the scores of its neighbors.

For each neighbor, we will calculate their next row and next column values using the neighbors' list we made previously.

If those values are in bounds and unseen then we will mark them as seen, calculate the minimum score between them and the current cell, and push them into the heap next with the time cost being what the heap sorts on so that we can continuously pick the cells with the largest, minimum scores.

In other words, we won't fall into a lesser score path unless we have no larger minimum score in the path.  This way, we are choosing the greatest values during our traversal.

            for neighbor in neighbors:
                next_row, next_col = row+neighbor[0], col+neighbor[1]
                if in_bounds(next_row, next_col):
                    seen[(next_row, next_col)] = True
                    next_score = min(-score, grid[next_row][next_col])
                    heapq.heappush(heap, (-next_score, next_row, next_col))

---