Swim in Rising Water

Patrick Leaton

Published: Oct. 7, 2021, 10:35 p.m.

Problem Description

You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).

The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.

Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).

Example 1:

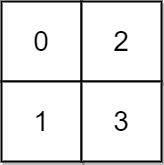
Input: grid = [[0,2],[1,3]]
Output: 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.

Example 2:

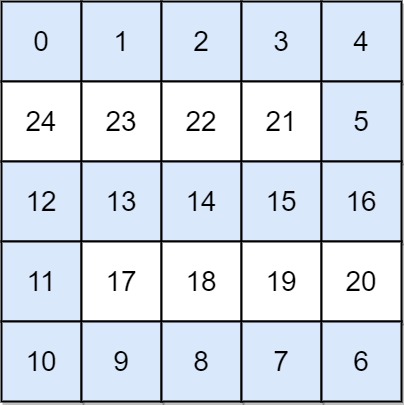
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation: The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.

Constraints:

n == grid.length
n == grid[i].length
1 <= n <= 50
0 <= grid[i][j] < n^2
Each value grid[i][j] is unique.

The description was taken from https://leetcode.com/problems/swim-in-rising-water/.

Problem Solution

#O(N^2(Log(N))) Time, O(N^2) Space

class Solution:

    def swimInWater(self, grid: List[List[int]]) -> int:

        heap, seen = [], {}

        neighbors = [(0,1),(1,0),(-1,0),(0,-1)]

        n = len(grid)

        

        def in_bounds(row:int, col:int) -> bool:

            if row < 0 or col < 0 or row >=n or col >=n:

                return False

            if (row, col) in seen:

                return False

            return True

        

        heap.append((grid[0][0],0,0))

        seen[(0,0)] = True

        while heap:

            t, row, col = heapq.heappop(heap)

            if (row, col) == (n-1, n-1):

                return t

            for neighbor in neighbors:

                next_row, next_col = row+neighbor[0], col+neighbor[1]

                if in_bounds(next_row, next_col):

                    seen[(next_row, next_col)] = True

                    next_t = max(t, grid[next_row][next_col])

                    heapq.heappush(heap, (next_t, next_row, next_col))

Problem Explanation

If we are given a matrix and are asked to find the shortest path, that is typically an indication that Breadth-First Search will be implemented.

However, since each cell contains a time cost to swim to their elevation, this is almost like being handed a matrix with weighted points. We wouldn't want to explore every neighbor cell to find the shortest path, but the cells with the least time costs that we'd have to wait to swim to them which are adjacent to the current one.

To solve this, we can perform a BFS but through the implementation of a heap instead of a queue. This will allow us to continuously pick the next cell with the shortest time cost and traverse the least costly path through the matrix. This could be considered a variation of Dijkstra's algorithm.

Let's start by initializing our heap and dictionary for seen cells.

heap, seen = [], {}

We'll also want to create a list of delta neighbor coordinates for the four surrounding cells of each cell. We can utilize these values later to calculate all four neighbors of a given cell.

neighbors = [(0,1),(1,0),(-1,0),(0,-1)]

Let's also want to cache the length and width of the grid so that we don't have to keep rewriting this later.

n = len(grid)

Here, we'll go ahead and make a helper function to let us know if the neighbor we are about to visit is valid.

If the row or column is outside the bounds of the array or has already been visited, the function will return false. Otherwise, it will return true.

def in_bounds(row:int, col:int) -> bool: if row < 0 or col < 0 or row >=n or col >=n: return False if (row, col) in seen: return False return True

Now we can begin our BFS.

We'll start with the first cell, so we will put its elevation time, row, and column into the heap then mark the row and column as seen.

heap.append((grid[0][0],0,0)) seen[(0,0)] = True

While we still have cells we need to visit in the heap, we are still swimming.

while heap:

We'll start each iteration off by popping the cell with the least time cost that we'd have to wait to swim to it.

If that cell is the last cell of the matrix, we will return the total time it cost to travel this shortest path.

t, row, col = heapq.heappop(heap) if (row, col) == (n-1, n-1): return t

Otherwise, we will look at the time costs of its neighbors.

For each neighbor, we will calculate their next row and next column values using the neighbors list we made previously.

If those values are in bounds and unseen then we will mark them as seen, calculate the max time cost between them and the current cell, and push them into the heap next with the time cost being what the heap sorts on so that we can continuously pick the cells with the lowest time cost to travel to.

for neighbor in neighbors: next_row, next_col = row+neighbor[0], col+neighbor[1] if in_bounds(next_row, next_col): seen[(next_row, next_col)] = True next_t = max(t, grid[next_row][next_col]) heapq.heappush(heap, (next_t, next_row, next_col))