Min Cost to Connect All Points

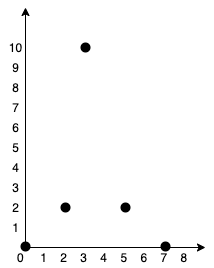
Input: points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
Output: 20
Explanation:

We can connect the points as shown above to get the minimum cost of 20.
Notice that there is a unique path between every pair of points.

Input: points = [[3,12],[-2,5],[-4,1]]
Output: 18

Input: points = [[0,0],[1,1],[1,0],[-1,1]]
Output: 4

Input: points = [[-1000000,-1000000],[1000000,1000000]]
Output: 4000000

Input: points = [[0,0]]
Output: 0

---

This problem is very similar to Connecting Cities With Minimum Cost.  We are given a set of coordinates which when connected, would create an undirected weighted graph and are asked for the minimum cost to connect all of the points.

This type of problem belongs in the category of Minimum Spanning Trees.

There are many ways to solve these, but maybe one of the more intuitive solutions is Prim's algorithm, a variation of Dijkstra's which we can use to find the minimum cost to connect the shortest paths of each node by traversing each shortest path. 

---

Let's start by initializing our adjacency list which we will use to map each node to its neighbors, and our dictionary for nodes that we have seen.

        adjacency, seen = {}, {}

 

We will also need a counter that we'll output which we will increment by the weights of the shortest paths we travel.

        output = 0

 

Let's go ahead and step through the list of nodes and initialize an empty list for each node that we will fill with its neighbors in a moment.

        for node in range(len(points)):
            adjacency[node] = []

 

For each point, we are going to need to create an edge to each other point within the adjacency list.  

Let's take the x and y coordinates from the first point for each point in the list.

        for point_one in range(len(points)):
            x_one, y_one = points[point_one]

 

Then, we will take the x and y coordinates from the second point for each other point in the list.  We will calculate the Manhattan distance using the formula provided in the problem description then add that to the adjacency list along with the edges.

Since we are creating an edge to and from each point, we can start from the coordinate directly after the first point for each second point because we won't have to revisit points.  An edge to go back to the first point will be required since this is an undirected graph we are building so that we can travel among various routes to each node.

            for point_two in range(point_one+1, len(points)):
                x_two, y_two = points[point_two]
                cost = abs(x_one - x_two) + abs(y_one - y_two)
                adjacency[point_one].append((cost, point_two))
                adjacency[point_two].append((cost, point_one))

 

Next, we will begin our shortest path traversal starting from the first node.

We will initialize a heap with a tuple of zero and zero.  We are choosing node zero as the source node so it will have an initial cost of zero to travel to it.

        heap = [(0,0)]

 

While the length of nodes we have seen is less than the length of nodes in the graph, we will continue traversing the shortest paths to visit each node.

        while len(seen) < len(points):

 

Each iteration will begin by popping the current shortest path between any two nodes from the heap and if we have seen the destination node before, we will skip it so that we don't revisit it.

If we have already seen it before, that means we have also seen a shorter path to it already.

            cost, node = heapq.heappop(heap)
            if node in seen:
                continue

 

If not, we will mark it as seen, increment the output by the cost to get to it so that we are essentially traveling the path, and if we have not seen its neighbors, we will push them into the heap next with the cost to travel the path to them.

            seen[node] = True
            output += cost
            for path_cost, neighbor in adjacency[node]:
                if neighbor not in seen:
                    heapq.heappush(heap, (path_cost, neighbor))

 

Once we have broken from the loop, we will have popped and traveled the shortest path to visit each node so all of the longer paths will be left on the heap.

We'll now return the output that will let us know the cost to travel each shortest path.

        return output

---