Parallel Courses

Patrick Leaton

Published: Oct. 5, 2021, 8:28 p.m.

Problem Description

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei.

In one semester, you can take any number of courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.

Return the minimum number of semesters needed to take all courses. If there is no way to take all the courses, return -1.

Example 1:

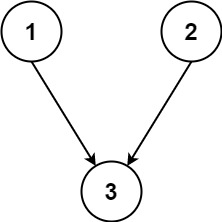
Input: n = 3, relations = [[1,3],[2,3]]
Output: 2
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 1 and 2.
In the second semester, you can take course 3.

Example 2:

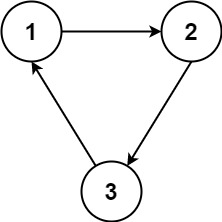
Input: n = 3, relations = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: No course can be studied because they are prerequisites of each other.

Constraints:

1 <= n <= 5000
1 <= relations.length <= 5000
relations[i].length == 2
1 <= prevCoursei, nextCoursei <= n
prevCoursei != nextCoursei
All the pairs [prevCoursei, nextCoursei] are unique.

The description was taken from https://leetcode.com/problems/parallel-courses/.

Problem Solution

#O(V+E) Time, O(V+E) Space

class Solution:

    def minimumSemesters(self, n: int, relations: List[List[int]]) -> int:

        adjacency, to_pointers = {}, {}

        queue = collections.deque()

        output, seen = 0, 0

        

        for node in range(1, n+1):

            adjacency[node] = set()

            to_pointers[node] = 0

        

        for node, neighbor in relations:

            adjacency[node].add(neighbor)

            to_pointers[neighbor] += 1

        

        for node in to_pointers:

            if not to_pointers[node]:

                queue.append(node)

                

        while queue:

            width = len(queue)

            for _ in range(width):

                node = queue.popleft()

                seen += 1

                for neighbor in adjacency[node]:

                    to_pointers[neighbor] -= 1

                    if not to_pointers[neighbor]:

                        queue.append(neighbor)

            output += 1

        

        if seen != n:

            return -1

        

        return output

Problem Explanation

If we are given a problem and are required to visit the cells, nodes, or characters that have no parent values, in this case, no prerequisite courses, that is typically an indication that a topological sort could be implemented.

A topological sort is a Breadth-First Search or Depth-First Search where either parentless nodes or childless nodes depending on the task, are visited first before any other ones to determine if a solution can be found.

We're looking for the shortest path in this graph since we're wanting to return the minimum number of semesters required, this could be rephrased as the number of levels traversed. A BFS is usually more favorable in finding the shortest path than a DFS is.

To solve this problem, we can find each course that has no prerequisites and visit them first within a BFS. Once we have done that, we will remove them from our list of courses to take so their next course will then have no prerequisites.

This process would continue until we were able to visit each course in order or had to drop out due to there being courses that were prerequisites for each other.

Let's start by initializing our adjacency list for the mapping of each prerequisite course to its next course, our to_pointers list which will contain each node that has a prerequisite course, and our queue for our BFS.

adjacency, to_pointers = {}, {} queue = collections.deque()

We will also need a counter for the number of semesters that passed during our BFS and how many courses we were able to take.

output, seen = 0, 0

Next, let's go through each course node and place initialize their place within our adjacency and to_pointers lists.

for node in range(1, n+1): adjacency[node] = set() to_pointers[node] = 0

Then, we will traverse the list of relations and point each prerequisite course node to its next course node within our adjacency list and increment the number of edges the next course has pointing to it by one.

for node, neighbor in relations: adjacency[node].add(neighbor) to_pointers[neighbor] += 1

Next, we will look for the first layer to visit within our BFS.

If we walk through our list of nodes that have no other nodes pointing to them, meaning they are courses with no prerequisites, we will visit them first.

for node in to_pointers: if not to_pointers[node]: queue.append(node)

Now we can begin our BFS if we have nodes in our queue.

While we still have courses we need to take, we will calculate the width of our queue to let us know how many courses we have in a given semester.

while queue: width = len(queue)

Then, for each course in that semester, we will pop its node from our queue, mark that we have seen an additional course, and for each node this course was a prerequisite for, we will subtract the number of edges pointing at them to remove this course from our search.

for _ in range(width): node = queue.popleft() seen += 1 for neighbor in adjacency[node]: to_pointers[neighbor] -= 1

If they now have no prerequisites after removing this course, we will visit them next.

if not to_pointers[neighbor]: queue.append(neighbor)

Once we have traversed each node within a semester, we will increment the output by one.

output += 1

If the number of seen courses does not equal the number of courses given, that means we weren't able to take all of the courses due to there being cycles in prerequisites.

if seen != n: return -1

Otherwise, we'll return the output which will tell the minimum number of semesters that needed to be taken.

return output