Reorder Routes to Make All Paths Lead to the City Zero

Patrick Leaton

Published: Oct. 3, 2021, 11:35 p.m.

Problem Description

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.

This year, there will be a big event in the capital (city 0), and many people want to travel to this city.

Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.

It's guaranteed that each city can reach city 0 after reorder.

Example 1:

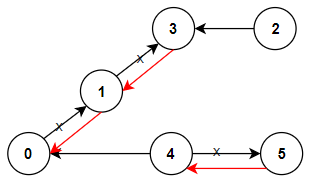
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3:

Input: n = 3, connections = [[1,0],[2,0]]
Output: 0

Constraints:

2 <= n <= 5 * 10^4
connections.length == n - 1
connections[i].length == 2
0 <= ai, bi <= n - 1
ai != bi

The description was taken from https://leetcode.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/.

Problem Solution

#O(N) Time, O(N) Space

class Solution:

    def minReorder(self, n: int, connections: List[List[int]]) -> int:

        adjacency, seen, paths = {}, {}, {}

        

        for node in range(n):

            adjacency[node] = []

            seen[node] = False

            

        for node, neighbor in connections:

            adjacency[node].append(neighbor)

            adjacency[neighbor].append(node)

            paths[(node, neighbor)] = True

            

        def bfs(node:int) -> int:

            changes = 0

            queue = collections.deque([(node)])

            seen[node] = True

            while queue:

                node = queue.popleft()

                for neighbor in adjacency[node]:

                    if seen[neighbor]:

                        continue

                    seen[neighbor] = True

                    if (neighbor, node) not in paths:

                        changes += 1

                    queue.append(neighbor)

            return changes

        

        return bfs(0)

Problem Explanation

From the diagrams in the problem description, we can see that the only edges that need to be changed are all the ones pointing away from the direction to zero.

To change this, we can map each set of paths between nodes and perform a traversal through the graph. Each time we see that there isn't a path from a neighbor to the current node, we will require an additional change to create that path so we will increment a counter.

Let's create a dictionary for the adjacency list, nodes we have seen, and paths between node pairs.

adjacency, seen, paths = {}, {}, {}

Next, let's go ahead and initialize the adjacency list of each node and set their initial values as false in the seen dictionary.

We could avoid doing this if we instead used Python's collections' default dictionary but it's just one additional traversal so it won't bog down the time complexity of our algorithm at all.

for node in range(n): adjacency[node] = [] seen[node] = False

Then, we will go through each node and its neighbor within the connections list and make the mapping between them.

We'll also want to map the connection within the paths dictionary so that we can tell if we need any additional paths later on.

for node, neighbor in connections: adjacency[node].append(neighbor) adjacency[neighbor].append(node) paths[(node, neighbor)] = True

Now we just need our BFS function.

def bfs(node:int) -> int:

Let's initialize the number of changes we need as zero, push the source node into the queue, and mark the source node as seen.

changes = 0 queue = collections.deque([(node)]) seen[node] = True

We'll now begin our BFS.

While we have nodes in the queue, our BFS will continue.

while queue:

During our BFS, we will pop a node and begin looking at its neighbors.

node = queue.popleft() for neighbor in adjacency[node]:

If we encounter a neighbor that we have visited before, we will continue to the next one.

if seen[neighbor]: continue

Otherwise, we will mark the neighbor as seen and check if we have an edge from the neighbor to the current node within our paths.

If we don't, we'll need to change that so that the neighbor node can reach node zero. We'll increment our required changes by one and append the neighbor to the queue so we can visit its neighbors next.

seen[neighbor] = True if (neighbor, node) not in paths: changes += 1 queue.append(neighbor)

Once we have visited each node in the graph, we will return the number of changes to the directions required so that each node can reach node zero.

return changes

Now that we have our BFS function built, we just need to make the initial call to visit node zero first.

return bfs(0)