Binary Tree Vertical Order Traversal

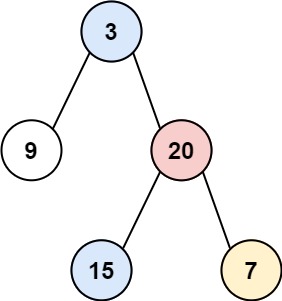
Input: root = [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]

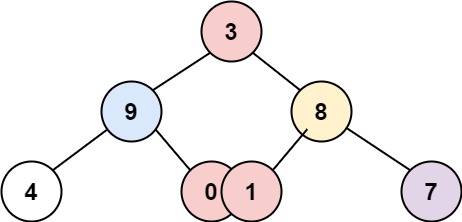
Input: root = [3,9,8,4,0,1,7]
Output: [[4],[9],[3,0,1],[8],[7]]

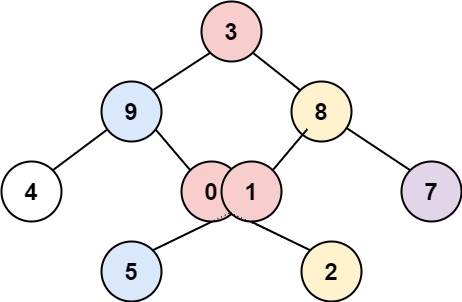
Input: root = [3,9,8,4,0,1,7,null,null,null,2,5]
Output: [[4],[9,5],[3,0,1],[8,2],[7]]

Input: root = []
Output: []

---

Breadth-First Search

Similar to the other funky level order traversal problems, we are going to need a hashmap or some other kind of external memory to group each node by an identifier, in this case, their vertical column value.

What we can do is utilize a BFS to traverse the tree from top to bottom and each time we append a child node to the queue, we will append a column value relative to the current node's column value.  Initially, this will be zero for the root, a negative one for the root's left child, and plus one for the root's right child.

Through those vertical column values, we will be able to group each node that shares the same column within the hashmap.

Once we have those groupings, we can traverse the hashmap and append each vertical column to the output array.

---

First off, if we have no root then we have no vertical order traversal so we will return an empty list.

        if not root:
            return []

 

Otherwise, we will initialize our vertical column hashmap and output array.

        verticals = {}
        output = []

---

Next, we will create our bfs function.

        def bfs(root:TreeNode, col:int) -> None:

 

We'll initialize our queue with the root and zeroth vertical column value that the root resides in.

            queue = collections.deque([(root, 0)])

 

While the queue has nodes to process, we will pop off a node, either append the node value to the vertical column if it already exists or initialize the column with the node value and if the node has children, we will append them to the queue next.  We'll need to decrement the current column value for a left child and increment it for a right child.

            while queue:
                node, col = queue.popleft()
                if col not in verticals:
                    verticals[col] = [node.val]
                else:
                    verticals[col].append(node.val)
               
                if node.left:
                    queue.append((node.left, col-1))
                if node.right:
                    queue.append((node.right, col+1))

 

Now that we have our BFS function made, we will make the initial call to fill the hashmap with all of the vertical column groups.

        bfs(root, 0)

 

Here is a tricky part.

We need to output the vertical columns in ascending order, but we don't know all of the vertical columns we could have.  We can't just iterate through a traditional range because for example, example one's vertical column values will range from a negative one to two.

The easy thing would be to sort the keys of the dictionary and traverse through them, but that would drop our time complexity from linear to O(N(Log(N)).  

A solution is to make a list of the keys that we can then find the minimum and maximum of to know what vertical columns we need to traverse.

        vertical_range = verticals.keys()
        col_min, col_max = min(vertical_range), max(vertical_range)

 

Once we have our range of the minimum vertical column identifier and the maximum, we will traverse each column and append the group of nodes that belong to the column.

        for vertical in range(col_min, col_max+1):
            output.append(verticals[vertical])

 

Once we have finished appending each grouping, we will return the output.

        return output

---

---

Depth-First Search

The DFS implementation is a little trickier to implement.  The reason being, we are no longer traversing the tree top to bottom, but instead depth-first.  By doing that, if we tried to just swap the queue for a call stack, it wouldn't work because some vertical columns would have the deeper nodes traversed first.  

To solve this, we will also need a row identifier to know how high a node is within its vertical column.

        def dfs(node:TreeNode, row:int, col:int) -> None:
            if not node:
                return
            if col not in verticals:
                verticals[col] = [(row, node.val)]
            else:
                verticals[col].append((row, node.val))
            dfs(node.left, row+1, col-1)
            dfs(node.right, row+1, col+1)

 

That's the first trick.

The second trick is we are going to need to sort the vertical columns by the row identifier so that each vertical column is ordered top to bottom.

Not only that, but we are going to need to strictly sort on the row value due to the description saying that nodes that belong in the same row and column should be ordered from left to right.  That means that if we were to use a normal sort function or a heap, the nodes with the same row and column values would be sorted first on the row, then on their values, which would result in them being sorted by their node values.  That wouldn't work because we need them sorted left to right, not by node values.  

To solve this, we will use a lambda function to sort strictly by row values.

We'll traverse the verticals hashmap similar to the BFS solution, but once we get to each column, we will need to sort the column by the row which is the first index in the pair tuples.

We can then go through the column and append each node to a bucket that we will then append the output.

            bucket = []
            verticals[vertical].sort(key=lambda x:x[0])
            for row, node in verticals[vertical]:
                bucket.append(node)
            output.append(bucket)

---