Problem Description
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
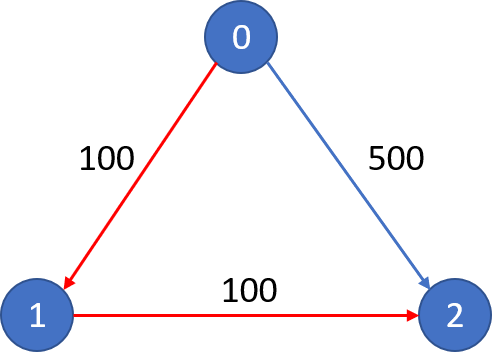
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown. The cheapest price from city0to city2with at most 1 stop costs 200, as marked red in the picture.
Example 2:

Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown. The cheapest price from city0to city2with at most 0 stop costs 500, as marked blue in the picture.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
The description was taken from https://leetcode.com/problems/cheapest-flights-within-k-stops/.
Problem Solution
#O(E*K) Time, O(N) Space
class Solution:
def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
prices = [float("inf") for _ in range(n)]
prices[src] = 0
for _ in range(k + 1):
temp_prices = list(prices)
for source, dest, price in flights:
flight_price = prices[source] + price
if flight_price < temp_prices[dest]:
temp_prices[dest] = flight_price
prices = temp_prices
if prices[dst] != float("inf"):
return prices[dst]
else:
return -1Problem Explanation
We are given a graph with weighted edges and are asked to return the shortest path to a destination.
Typically for questions like this, a rule of thumb is to use Dijkstra's algorithm until it fails, in which case to use Bellman-Ford's. Typically this scenario is when the graph has negative edges, but the limitation of stops won't allow Dijkstra's to work as intended. This is because Dijkstra's algorithm does not revisit each node within each iteration, but Bellman-Ford's does.
With Bellman-Ford's algorithm, each node is visited a total of len(nodes) -1 times, the intention being that each extra visit through all the of nodes will update a shorter path.
If the paths we are able to update to a shorter path are limited to the number of stops we have, then the only major tweak we need to make to Bellman-Ford's, besides needing to run it twice to account for negative cycles which there are none here, is we will visit each node k times That way, we are only updating a shorter path whenever we have a stop available.
Let's start by creating the prices array that will hold the price to get to each node, we will set the source price to zero because it costs nothing to start from the first city.
prices = [float("inf") for _ in range(n)]
prices[src] = 0
Now let's have a loop that will let us visit each node as many times as there are stops.
for _ in range(k + 1):
Before we go through an iteration of visiting each node, we will need to create a temporary prices list so that we don't relax a new edge until the next iteration.
temp_prices = list(prices)
Then, for each source city, destination city, and flight price in the flights array, we will calculate the current cost to the destination city by first referencing our cheapest flight to get to the source and adding the flight price to it.
If that cost is cheaper than the one we have saved, we will update it within the temporary array, relaxing this edge.
for source, dest, price in flights:
flight_price = prices[source] + price
if flight_price < temp_prices[dest]:
temp_prices[dest] = flight_price
Once we have relaxed each node in the iteration, we copy the temporary prices list to the prices list and move to the next iteration where we can relax the additional edges if we have an additional stop.
prices = temp_prices
This will look something like this, we will initialize the prices list with the source and two destination nodes.
[0, inf, inf]
We will make our initial flight with zero stops, which will allow us to relax our immediate edges.
[0, 100, 500]
Next, we will relax the edges that would be available if we had one stop.
[0, 100, 200]
The pattern is being able to relax an immediate edge from the source, then being able to match the closest external edges, then being able to match the second closest external edges, each with an extra stop.
The reason for the temp prices array is the number of edges we can relax is limited to the number of stops we have, if we are relaxing an edge that exceeds the number of stops we have, that is equivalent to taking a path that we actually didn't have enough stops for.
If we have a destination node that was still infinity, by the time we completed our stops, that means that we didn't have enough stops to reach the destination in which case we will return a negative one.
if prices[dst] != float("inf"):
return prices[dst]
else:
return -1