Number of Provinces

Patrick Leaton

Published: Sept. 28, 2021, 12:04 a.m.

Problem Description

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

Example 1:

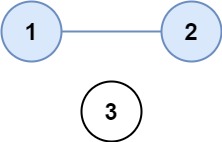
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

Example 2:

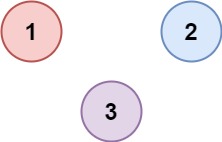
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

Constraints:

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] is 1 or 0.
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

The description was taken from https://leetcode.com/problems/number-of-provinces.

Problem Solution

#Recursive DFS

#O(N^2) Time, O(N) Space

class Solution:

    def findCircleNum(self, isConnected: List[List[int]]) -> int:

        seen = {}

        nodes = len(isConnected)

        def dfs(node:int) -> None:

            seen[node] = True

            for neighbor in range(nodes):

                if isConnected[node][neighbor] and neighbor not in seen:

                    dfs(neighbor)

        

        count = 0

        for node in range(nodes):

            if node not in seen:

                dfs(node)

                count += 1

        return count

#Iterative BFS

#O(N^2) Time, O(N) Space

class Solution:

    def findCircleNum(self, isConnected: List[List[int]]) -> int:        

        seen = {}

        nodes = len(isConnected)

        

        def bfs(node:int) -> None:

            queue = collections.deque([node])

            while queue:

                width = len(queue)

                for _ in range(width):

                    curr_node = queue.popleft()

                    seen[curr_node] = True

                    for neighbor in range(nodes):

                        if isConnected[curr_node][neighbor] and neighbor not in seen:

                            queue.append(neighbor)

        

        count = 0

        for node in range(nodes):

            if node not in seen:

                bfs(node)

                count +=1

        return count

Problem Explanation

Depth-First Search

This problem has the same solution as Number of Components in an Undirected Graph, with the only exception being the adjacency matrix we are given is slightly different.

Similar to that problem, the provinces we are given are basically different mini graphs. In order to count how many different graphs there are, we can iterate through each node, and each time we encounter a new node that we haven't seen, we will stop and perform a DFS on it and its neighbors, exhausting the graph it belongs to. That way, when we see a new node in any iteration afterward when we repeat the process, we know that it wasn't a part of any graphs we have already seen and this makes it easy for us to count how many different mini graphs, provinces we have.

Let's start by initializing our hashmap of nodes that we have seen and caching the length of how many connection arrays we have in our input because this will tell us how many nodes we need to iterate through.

seen = {} nodes = len(isConnected)

Next, we will create our recursive, dfs function.

Our function will take a node index and mark it as seen, then it will look through each value in the node's connection array, and if we see that the current node's connection list has a value of one in an index besides itself, meaning we have a connection to a different node, and if that node has not been seen before, we will continue our DFS on that neighbor node.

seen[node] = True for neighbor in range(nodes): if isConnected[node][neighbor] and neighbor not in seen: dfs(neighbor)

Let's draw this out.

In the first example we are looking at this adjacency matrix:

[[1,1,0],[1,1,0],[0,0,1]]

We would take node one as the initial DFS input:

[[1,1,0],[1,1,0],[0,0,1]]

We would mark node one as seen, then we would iterate through its neighbors, and if we saw that we had a connection to a neighbor like we do with two, then we would continue the DFS on node two.

[[1,1,0],[1,1,0],[0,0,1]]

Once we have our DFS function built, we will iterate through the number of nodes we have, and each time we encounter a node, we will send it into our DFS function and exhaust the mini graph it belongs to. We can then increment the count.

        for node in range(nodes):

            if node not in seen:

                dfs(node)

count += 1

Once we have traversed each node, we will return the number of times we had to run the DFS function to explore each province.

return count

Breadth-First Search

The BFS approach will be the same as the DFS approach, we just need to swap out the functions so that we use a queue to explore neighbors instead of a recursive call stack.

Everything will be the same up until we send an unseen node into the BFS function to explore each of its neighbors. At that point, we will push the node onto a queue within our BFS function. While we have nodes in the queue, we will pop a node, mark it as seen, and if we have a connection to a neighbor and the neighbor has not been seen, we will push the neighbor onto the queue.

def bfs(node:int) -> None: queue = collections.deque([node]) while queue: width = len(queue) for _ in range(width): curr_node = queue.popleft() seen[curr_node] = True for neighbor in range(nodes): if isConnected[curr_node][neighbor] and neighbor not in seen: queue.append(neighbor)