Problem Description
There is a ball in a maze with empty spaces (represented as 0) and walls (represented as 1). The ball can go through the empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the m x n maze, the ball's start position and the destination, where start = [startrow, startcol] and destination = [destinationrow, destinationcol], return true if the ball can stop at the destination, otherwise return false.
You may assume that the borders of the maze are all walls (see examples).
Example 1:
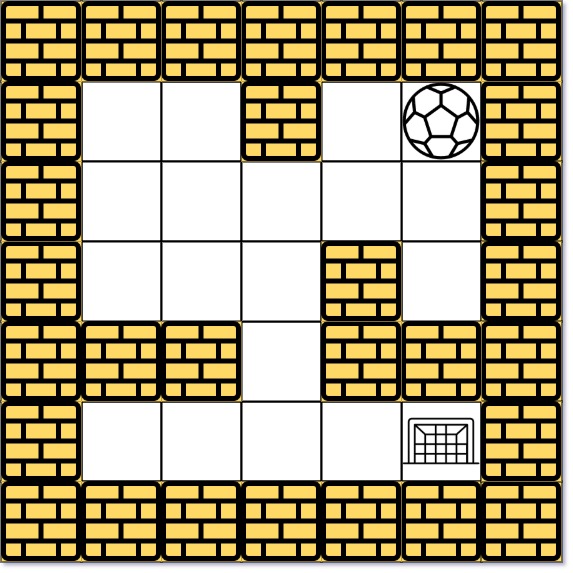
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4] Output: true Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
Example 2:
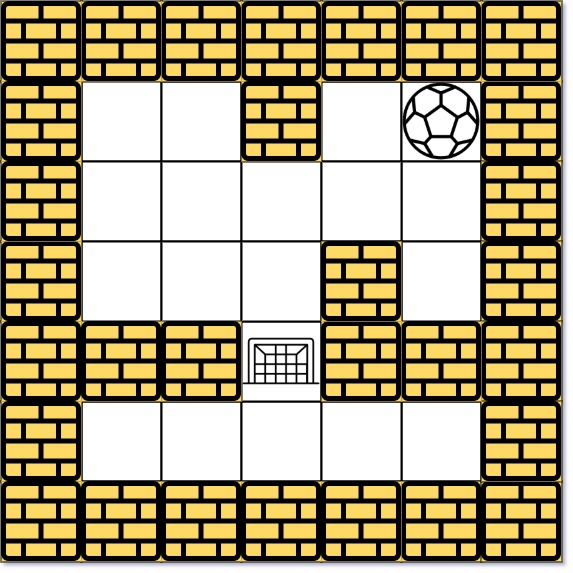
Input: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2] Output: false Explanation: There is no way for the ball to stop at the destination. Notice that you can pass through the destination but you cannot stop there.
Example 3:
Input: maze = [[0,0,0,0,0],[1,1,0,0,1],[0,0,0,0,0],[0,1,0,0,1],[0,1,0,0,0]], start = [4,3], destination = [0,1] Output: false
Constraints:
m == maze.lengthn == maze[i].length1 <= m, n <= 100maze[i][j]is0or1.start.length == 2destination.length == 20 <= startrow, destinationrow <= m0 <= startcol, destinationcol <= n- Both the ball and the destination exist in an empty space, and they will not be in the same position initially.
- The maze contains at least 2 empty spaces.
The description was taken from https://leetcode.com/problems/the-maze/.
Problem Solution
#O(M*N) Time, O(M*N) Space
class Solution:
def hasPath(self, maze: List[List[int]], start: List[int], destination: List[int]) -> bool:
m, n = len(maze), len(maze[0])
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >= n:
return False
if maze[row][col] != 0:
return False
return True
def bfs() -> bool:
queue = collections.deque([start])
seen = {}
neighbors = [(0,1),(1,0),(0,-1),(-1,0)]
seen[(start[0], start[1])] = True
while queue:
width = len(queue)
for _ in range(width):
row, col = queue.popleft()
if [row, col] == destination:
return True
for neighbor in neighbors:
roll_row, roll_col = row, col
while in_bounds(roll_row, roll_col):
roll_row += neighbor[0]
roll_col += neighbor[1]
last_valid = roll_row-neighbor[0], roll_col-neighbor[1]
if (last_valid) not in seen:
seen[(last_valid)] = True
queue.append((last_valid))
return False
return bfs()Problem Explanation
When we're given a matrix and are required to find either the shortest path or if a path exists, a Breadth-First Search is almost always better than a Depth-First Search in that a DFS will be taking detours where a BFS will draw a straight, linear path to the destination.
However, this problem requires us to roll until we hit a wall, which gives this problem a DFS requirement. To satisfy this requirement, we will not explore all four neighbors for each cell but instead, exhaust all four neighbors. When we do a BFS on a matrix, typically we just push each valid of the surrounding neighbors into the matrix so we get a layer-by-layer traversal of the matrix. What we will do here instead is continue down each neighbors path before visiting the next one, that way we get a BFS traversal of the matrix in a DFS manner.
Let's start by caching the length and width of the maze to variables m, and n, so that we don't have to keep calculating these values later on.
m, n = len(maze), len(maze[0])
Next, let's create a helper function that will let us know if our ball is in bounds.
If the ball has gone past the bounds of the matrix or has hit an obstacle, we will return false, otherwise, we will return true.
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >= n:
return False
if maze[row][col] != 0:
return False
return True
Next, let's create our BFS function.
def bfs() -> bool:
We will initialize our queue with the starting place and we will also create a hashmap to store the cells we have seen.
queue = collections.deque([start])
seen = {}
Within our function, we will create a list of delta neighbor coordinates for the eight surrounding cells of each cell. We can utilize these values later to calculate all four neighbors of a given cell.
neighbors = [(0,1),(1,0),(0,-1),(-1,0)]
Let's also mark the starting cell as seen so that we don't revisit it.
seen[(start[0], start[1])] = True
While we still have cells in the queue, we will continue our BFS, searching for the path to the destination.
while queue:
At the beginning of each iteration, we will calculate the length of the queue to know how many cells we need to empty from the queue.
width = len(queue)
For each cell in the queue, we will pop the row and column coordinates and check if they're the destination. If they are, then we will return the distance it took to travel to this cell.
for _ in range(width):
row, col = queue.popleft()
if [row, col] == destination:
return True
If not, we will continue searching its neighbors.
As mentioned previously, instead of adding the neighbors to the queue and continuing to the next iteration, we will continue rolling down a neighbor's path before moving to the next neighbor.
For example, the first tuple in the neighbors' list is (0,1), so keep incrementing our column value, rolling as far to the right as we can before we roll into a wall.
for neighbor in neighbors:
roll_row, roll_col = row, col
while in_bounds(roll_row, roll_col):
roll_row += neighbor[0]
roll_col += neighbor[1]
Once that has happened, we will mark our last valid spot as the spot we were at before we hit the wall.
last_valid = roll_row-neighbor[0], roll_col-neighbor[1]
If that spot hasn't been visited before, meaning we haven't placed it in or popped it from the queue yet to search its four directions, we will mark it as seen and add it to the queue so that we can roll down its four directions later.
if (last_valid) not in seen:
seen[(last_valid)] = True
queue.append((last_valid))
If we emptied the queue and never found the destination, then we didn't have a path to it so we will return false.
return False
Once we have finished building the function, all we need to do is make the initial call that will return whether or not we found a path to the destination.
return bfs()