Problem Description
Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.
A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:
- All the visited cells of the path are
0. - All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
The length of a clear path is the number of visited cells of this path.
Example 1:
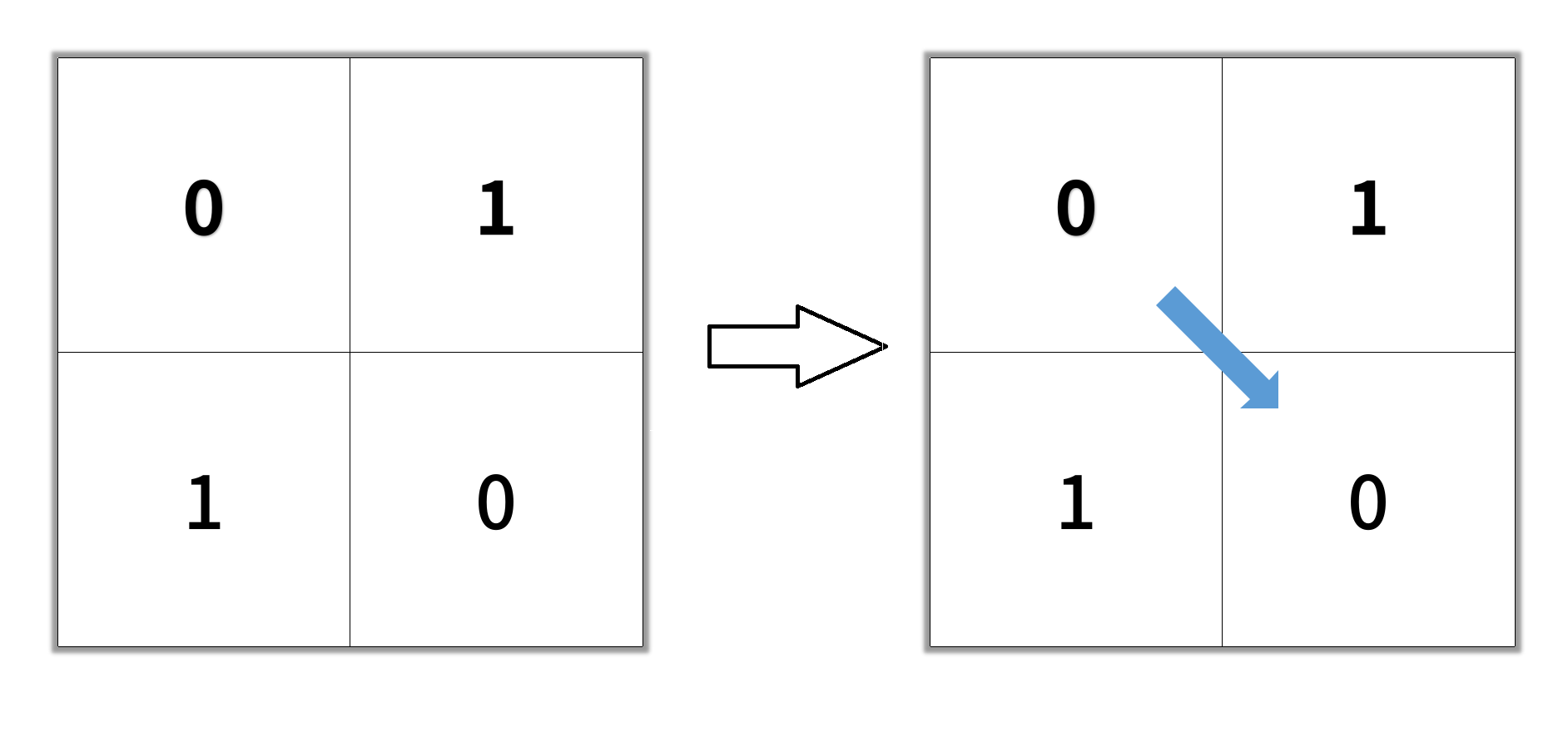
Input: grid = [[0,1],[1,0]] Output: 2
Example 2:
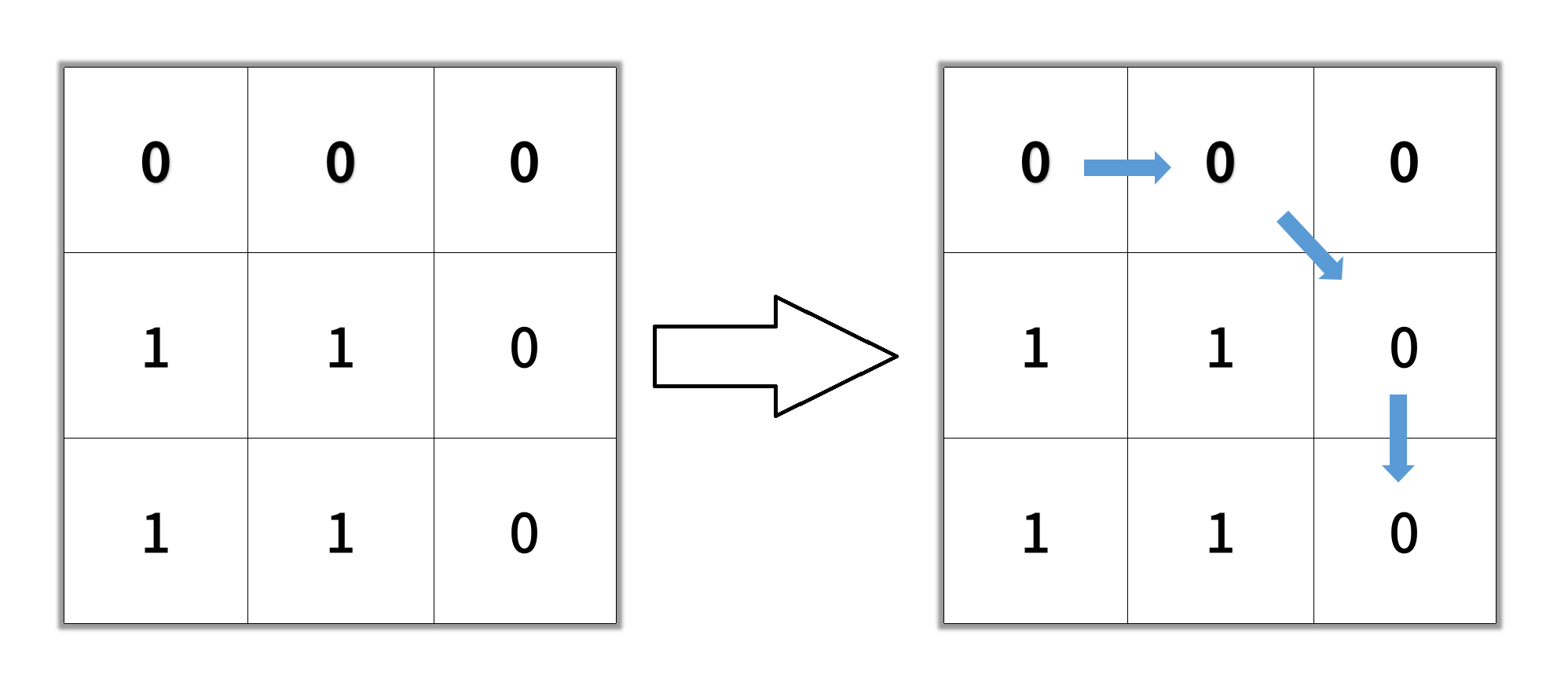
Input: grid = [[0,0,0],[1,1,0],[1,1,0]] Output: 4
Example 3:
Input: grid = [[1,0,0],[1,1,0],[1,1,0]] Output: -1
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 100grid[i][j] is 0 or 1
The description was taken from https://leetcode.com/problems/shortest-path-in-binary-matrix.
Problem Solution
#O(N^2) Time, O(N^2) Space
class Solution:
def shortestPathBinaryMatrix(self, grid: List[List[int]]) -> int:
if grid[-1][-1] == 1 or grid[0][0] == 1:
return -1
m, n = len(grid), len(grid[0])
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >=m or col >= n:
return False
if grid[row][col] == 1:
return False
return True
def bfs() -> int:
neighbors = [(0,1),(1,0),(0,-1),(-1,0),(-1,-1),(-1,1),(1,-1),(1,1)]
queue = collections.deque([(0,0)])
distance = 1
while queue:
width = len(queue)
for _ in range(width):
row, col = queue.popleft()
if (row, col) == (m-1, n-1):
return distance
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
queue.append((next_row,next_col))
grid[next_row][next_col] = 1
distance += 1
return -1
return bfs()Problem Explanation
When we're given a matrix and are required to find either the shortest path or if a path exists, a Breadth-First Search is almost always better than a Depth-First Search in that a DFS will be taking detours where a BFS will draw a straight, linear path to the destination.
What we will do is push the first cell into the queue and check the neighbors that are in the bounds of the array and are zero, if these two cases are valid then we will push them into the queue and explore their neighbors next. If we have emptied the queue and didn't get to the destination, then there isn't a path to it.
First off, if the first or last cell is blocked off then we have no way to get to the destination, so we will return a negative one.
if grid[-1][-1] == 1 or grid[0][0] == 1:
return -1
Otherwise, we will begin by caching the length and width of the matrix into two variables m, and n, so that we don't have to keep calculating these values.
m, n = len(grid), len(grid[0])
Next, we will go ahead and create a helper function that tests for valid cells.
It will take a row and column coordinate and will tell us if the cell is in the bounds of the matrix and whether it is a valid cell that we can travel to.
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >=m or col >= n:
return False
if grid[row][col] == 1:
return False
return True
After, we will create our standard BFS function.
def bfs() -> int:
Within our function, we will create a list of delta neighbor coordinates for the eight surrounding cells of each cell. We can utilize these values later to calculate all eight neighbors of a given cell.
neighbors = [(0,1),(1,0),(0,-1),(-1,0),(-1,-1),(-1,1),(1,-1),(1,1)]
Next, we will push the first cell into the queue and initialize our path distance to one, since in the examples the distance includes the first cell.
queue = collections.deque([(0,0)])
distance = 1
While we still have cells in the queue, we will continue our BFS, searching for the shortest path to the last cell by taking the roads of zeros.
while queue:
At the beginning of each iteration, we will calculate the length of the queue. This will let us know how big the current layer is so that we can increase the distance after that layer has been searched.
width = len(queue)
For each cell in the queue, we will pop the row and column coordinates and check if they're the last coordinates of the matrix. If they are, then we will return the distance it took to travel to this cell.
for _ in range(width):
row, col = queue.popleft()
if (row, col) == (m-1, n-1):
return distance
If not, we will continue searching its neighbors.
We can get the next row and column for each neighbor by summing each tuple within the neighbors' array with the current row and column.
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
For each neighbor, if they are in bounds and are zero then we will add them to the queue, mark them as one so that we don't revisit them, and we will visit them when we search the next layer.
if in_bounds(next_row, next_col):
queue.append((next_row,next_col))
grid[next_row][next_col] = 1
Once we have emptied the queue for a given layer, we will increment the distance by one, since getting to the destination is now requiring one additional layer of searching.
distance += 1
If we emptied the queue and never got to the end of the matrix, we didn't have a path to get there so we will return a negative one.
return -1
Now, all we need to do is make the initial BFS function call.
return bfs()