Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts
Patrick LeatonProblem Description
You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts where:
horizontalCuts[i]is the distance from the top of the rectangular cake to theithhorizontal cut and similarly, andverticalCuts[j]is the distance from the left of the rectangular cake to thejthvertical cut.
Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a large number, return this modulo 109 + 7.
Example 1:
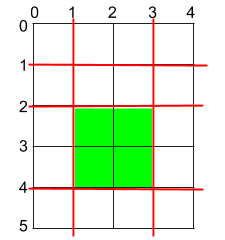
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] Output: 4 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
Example 2:
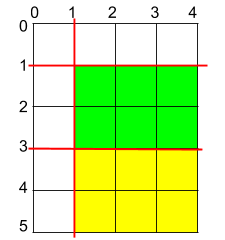
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] Output: 6 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
Example 3:
Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] Output: 9
Constraints:
2 <= h, w <= 1091 <= horizontalCuts.length <= min(h - 1, 105)1 <= verticalCuts.length <= min(w - 1, 105)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- All the elements in
horizontalCutsare distinct. - All the elements in
verticalCutsare distinct.
The description was taken https://leetcode.com/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts.
Problem Solution
#O(N(Log(N))) + M(Log(M))) Time, O(1) Space
class Solution:
def maxArea(self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int]) -> int:
horizontalCuts.sort()
verticalCuts.sort() max_height = max(horizontalCuts[0] - 0, h - horizontalCuts[-1])
for i in range(1, len(horizontalCuts)):
cut = horizontalCuts[i]
last_cut = horizontalCuts[i-1]
max_height = max(max_height, cut - last_cut)
max_width = max(verticalCuts[0] - 0, w - verticalCuts[-1])
for i in range(1, len(verticalCuts)):
cut = verticalCuts[i]
last_cut = verticalCuts[i-1]
max_width = max(max_width, cut - last_cut)
return (max_height * max_width) % (10**9 + 7)Problem Explanation
This problem is very similar to Container with Most Water.
Similar to that problem, this problem is going to utilize a somewhat greedy approach where we can find the greatest area. The components of an area are length and width.
What we can do is iterate through the horizontal cuts array to find the greatest width, then we can iterate through the vertical cuts array and find the greatest length. From there, all we need to do is multiply the greatest width we found by the greatest length we found to get the maximum slice of cake.
Let's order the lists of cuts so that we can traverse the lists and measure the distance between each consecutive cut.
horizontalCuts.sort()
verticalCuts.sort()
We will first measure the edge slices, this would be the distance between the first cut and the beginning of the cake, and the last cut and the end of the cake.
max_height = max(horizontalCuts[0] - 0, h - horizontalCuts[-1])
Now we will begin looking for the maximum length.
From the first cut to the last cut, we will measure the lengths between the cuts and try to find the maximum length.
for i in range(1, len(horizontalCuts)):
cut = horizontalCuts[i]
last_cut = horizontalCuts[i-1]
max_height = max(max_height, cut - last_cut)
We will do the same thing, but looking for the maximum width now.
max_width = max(verticalCuts[0] - 0, w - verticalCuts[-1])
for i in range(1, len(verticalCuts)):
cut = verticalCuts[i]
last_cut = verticalCuts[i-1]
max_width = max(max_width, cut - last_cut)
Once we find our maximum length and maximum width, we will calculate our maximum area modded by the number given in the description.
return (max_height * max_width) % (10**9 + 7)