Problem Description
Given an array of events where events[i] = [startDayi, endDayi]. Every event i starts at startDayi and ends at endDayi.
You can attend an event i at any day d where startTimei <= d <= endTimei. Notice that you can only attend one event at any time d.
Return the maximum number of events you can attend.
Example 1:
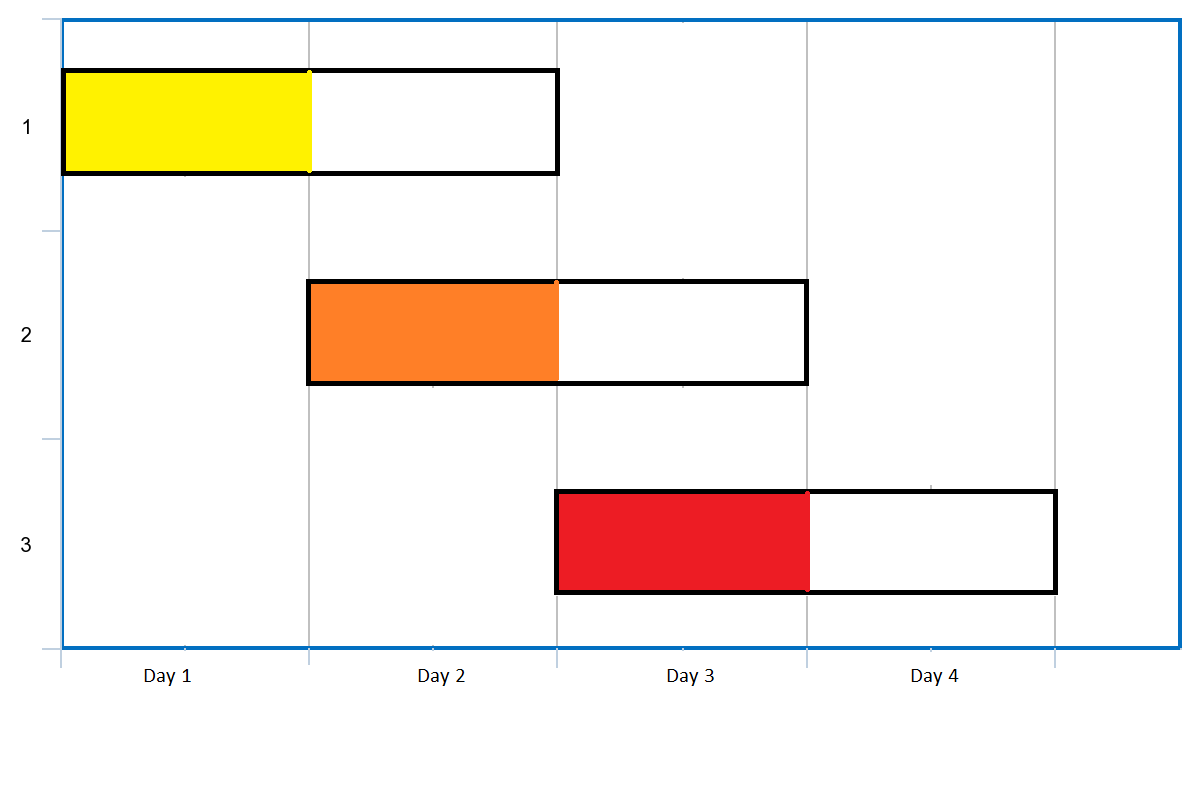
Input: events = [[1,2],[2,3],[3,4]] Output: 3 Explanation: You can attend all the three events. One way to attend them all is as shown. Attend the first event on day 1. Attend the second event on day 2. Attend the third event on day 3.
Example 2:
Input: events= [[1,2],[2,3],[3,4],[1,2]] Output: 4
Example 3:
Input: events = [[1,4],[4,4],[2,2],[3,4],[1,1]] Output: 4
Example 4:
Input: events = [[1,100000]] Output: 1
Example 5:
Input: events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]] Output: 7
Constraints:
1 <= events.length <= 10^5events[i].length == 21 <= startDayi <= endDayi <= 10^5
The description was taken from https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended.
Problem Solution
#O(N(Log(N))) Time, O(N) Space
class Solution:
def maxEvents(self, events: List[List[int]]) -> int:
intervals, heap = {}, []
attended = 0
latest_end = -1
for start, end in events:
if start not in intervals:
intervals[start] = [end]
else:
intervals[start].append(end)
latest_end = max(latest_end, end)
for start in range(1, latest_end + 1):
while heap and heap[0] < start:
heapq.heappop(heap) if start in intervals:
for end in intervals[start]:
heapq.heappush(heap, end)
if heap:
attended += 1
heapq.heappop(heap)
return attendedProblem Explanation
The description wants us to return the maximum number of events that can be attended.
That is a clue that this may be a greedy problem. Greedy problems take advantage of sorting the input and prioritizing the cheapest or most expensive tasks first, so that we may reserve the most resources.
In this case, the cheapest task would be the shortest intervals, and the resource we would like to conserve is our time.
What we can do is map each end time to each start time, and continuously pick the earliest end-time first. This allows us to choose the shortest intervals.
We will utilize a heap to achieve this goal.
Let's start by creating an intervals hashmap where we will map each end-time to their start-time so that we can choose the lesser one if there are duplicate events that start at the same time.
We will also initialize our heap here.
intervals, heap = {}, []
Next, we will need a running counter for the events we attend and a running latest_end value so we can keep track of how late our last event goes until and we know where we need to iterate to later.
attended = 0
latest_end = -1
Then, for each start time and end time in the events matrix, we will map each end time to the start time and update the latest end.
for start, end in events:
if start not in intervals:
intervals[start] = [end]
else:
intervals[start].append(end)
latest_end = max(latest_end, end)
Now we can start attending the events, so we will iterate through each day from the first to the latest.
for start in range(1, latest_end + 1):
We will start off by seeing if we have any events that have already ended before the current day. If we do, we will remove them from the heap since we won't be able to attend them anymore.
while heap and heap[0] < start:
heapq.heappop(heap)
Otherwise, if we have an event(s) that start today, then we will push their end times into the heap so that we can choose to attend the event that ends first. This will let us greedily attend the shorter intervals so that we can attend the most events.
if start in intervals:
for end in intervals[start]:
heapq.heappush(heap, end)
If we have events in the heap, we will attend the earliest ending event.
if heap:
attended += 1
heapq.heappop(heap)
Once we have reached the latest ending event, we will return the number of events we attended.
return attended