Shortest Path to Get Food

Input: grid = [["X","X","X","X","X","X"],["X","*","O","O","O","X"],["X","O","O","#","O","X"],["X","X","X","X","X","X"]]
Output: 3
Explanation: It takes 3 steps to reach the food.

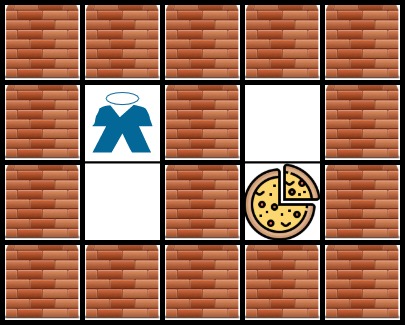
Input: grid = [["X","X","X","X","X"],["X","*","X","O","X"],["X","O","X","#","X"],["X","X","X","X","X"]]
Output: -1
Explanation: It is not possible to reach the food.

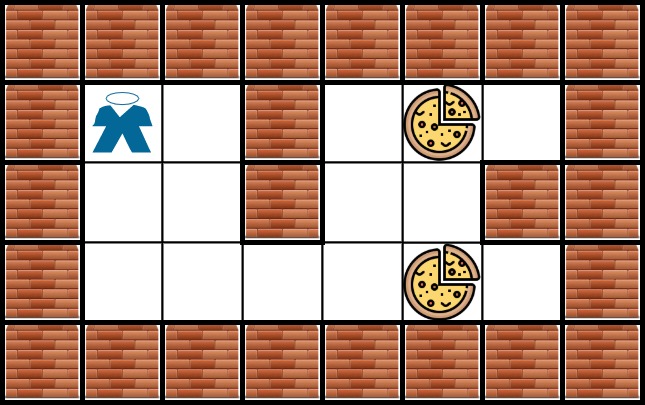
Input: grid = [["X","X","X","X","X","X","X","X"],["X","*","O","X","O","#","O","X"],["X","O","O","X","O","O","X","X"],["X","O","O","O","O","#","O","X"],["X","X","X","X","X","X","X","X"]]
Output: 6
Explanation: There can be multiple food cells. It only takes 6 steps to reach the bottom food.

Input: grid = [["O","*"],["#","O"]]
Output: 2

Input: grid = [["X","*"],["#","X"]]
Output: -1

---

Typically if we're trying to find the shortest path within a graph or matrix, a Breadth-First Search approach is favorable to a Depth-First Search since a DFS would be taking detours in the path instead of taking a linear, layer-by-layer path.

With that in mind, the approach will be fairly straightforward.  We will do a linear scan of the matrix, and when we find our starting point we will begin our BFS on the coordinates of that cell.  Once we find one of the pizzas, we will return the distance it took to get there.

---

Let's start things off by caching the length and width of the board to variables m and n, so that we don't have to keep recalculating these variables in each iteration.

        m, n = len(grid), len(grid[0])

---

Next, we will make a helper function that will take a row and column coordinate of a cell and return false if the cell is out of bounds or is an obstacle, otherwise, it will return true.

        def in_bounds(row:int, col:int) -> bool:
            if row < 0 or col < 0 or row >= m or col >= n:
                return False
            if grid[row][col] == "X":
                return False
            return True

---

Now we can make our BFS function that will take the row and column coordinates of the starting point.

        def bfs(row:int, col:int) -> int:

 

We will mark those coordinates as seen and add them to the queue so we can begin the BFS from there.

            seen = set((row,col))
            queue = collections.deque([(row,col)])

 

We will also want a counter that keeps track of the distance of the path taken to get to a pizza, and a list of neighbor deltas for the right, left, top, and bottom neighbors.

            distance = 0
            neighbors = [(0,1),(1,0),(-1,0),(0,-1)]

 

Now, we will write our BFS.

While we still have cells in our queue, we will continue searching for a path to the pizza.

            while queue:

 

Within our BFS, we will start by calculating the width of the queue because that will let us know how many cells are in the current layer.

                width = len(queue)
 

Then, within that layer, we will pop each cell from the queue and check if it is the pizza.

                for _ in range(width):
                    row, col = queue.popleft()
                    if grid[row][col] == "#":
                        return distance

 

If not, we will calculate its four neighbors and if they are in the bounds of the matrix and unseen, we will add them to the queue.

                    for neighbor in neighbors:
                        next_row, next_col = row+neighbor[0], col+neighbor[1]
                        if in_bounds(next_row, next_col) and (next_row, next_col) not in seen:
                            queue.append((next_row, next_col))
                            seen.add((next_row, next_col))

 

Once we have finished searching through an entire layer, we will increment the path distance by one and continue to the next layer.

                distance += 1

 

If we have emptied the queue and didn't find a pizza, that means there were obstacles keeping us from a pizza or there was no pizza.  If that is the case, we will return a negative one.

            return -1

---

Now that we have our functions built, we just need to make our initial scan, find the starting point and return the path distance of the BFS going from there.

        for row in range(m):
            for col in range(n):
                if grid[row][col] == "*":
                    return bfs(row, col)

---