Problem Description
According to Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."
The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
- Any live cell with fewer than two live neighbors dies as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population.
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously. Given the current state of the m x n grid board, return the next state.
Example 1:
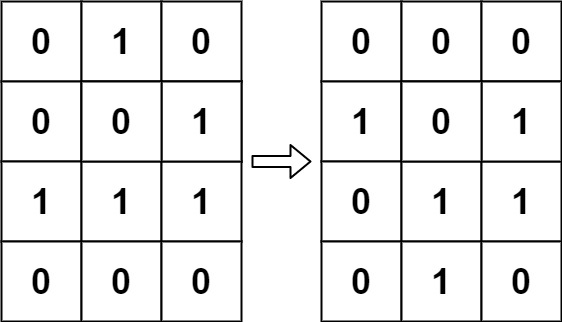
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
Example 2:
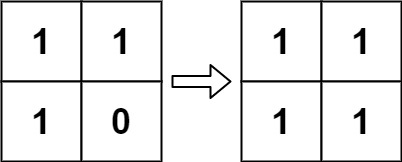
Input: board = [[1,1],[1,0]] Output: [[1,1],[1,1]]
Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 25board[i][j]is0or1.
Follow up:
- Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
- In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?
The description was taken from https://leetcode.com/problems/game-of-life/.
Problem Solution
#(M*N) Time, O(1) Space
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
m, n = len(board), len(board[0]) def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >= n:
return False
return True def count_neighbors(row:int, col:int) -> int:
neighbors = [(1,0),(0,1),(-1,0),(0,-1),(-1,-1),(-1,1),(1,-1),(1,1)]
lives = 0
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
if in_bounds(next_row, next_col):
if abs(board[next_row][next_col]) == 1:
lives += 1
return lives
def dead_or_alive(row:int, col:int, lives:int, now:int) -> int:
alive = board[row][col] == 1
if alive and lives < 2:
return -1
elif alive and lives > 3:
return -1 elif not alive and lives == 3:
return 2
else:
return now for row in range(m):
for col in range(n): now = board[row][col]
lives = count_neighbors(row,col)
board[row][col] = dead_or_alive(row, col, lives, now)
for row in range(m):
for col in range(n):
if board[row][col] > 0:
board[row][col] = 1
else:
board[row][col] = 0Problem Explanation
To solve this question is how it may seem. We could copy the board, iterate through each cell, then determine if it is dead or alive based on its current life status and the life status of its eight neighbors.
However, that would require an additional board's worth of space. The reason we needed to copy the board is that we need to know the current state of each cell which would be impossible to tell if we changed the state in place to a one or a zero. What we can do instead is use a different identifier for changed cells so that we know the state it was when the game started and we know what state it will be at the end.
The identifiers will remain zero and one for unchanged cells, two for cells that were dead but are now alive, and a negative one for cells that were alive but are now dead.
What we can do is make one traversal through the board and change the state of each cell that is now dead or alive based on its current life status and the status of its eight neighbors, then we can make a second traversal to decode those identifiers into a final result.
Let's start things off by caching the length and width of the board to variables m and n, so that we don't have to keep recalculating these variables in each iteration.
m, n = len(board), len(board[0])
Next, we are going to create a few helper functions.
The first will be one that will take a row and column coordinate then return whether the cell is within the bounds of the board.
def in_bounds(row:int, col:int) -> bool:
if row < 0 or col < 0 or row >= m or col >= n:
return False
return True
The next helper function will take a row and column coordinate then return how many of the neighbors of that cell are alive.
def count_neighbors(row:int, col:int) -> int:
We'll go ahead and make this neighbors list that will contain the delta coordinates to get all neighbors of the current cell.
neighbors = [(1,0),(0,1),(-1,0),(0,-1),(-1,-1),(-1,1),(1,-1),(1,1)]
We'll also want a counter for the number of lives the neighbors have.
lives = 0
Then, for each neighbor, we will calculate the next row and column coordinates by using the current coordinates and the delta coordinates.
for neighbor in neighbors:
next_row, next_col = row+neighbor[0], col+neighbor[1]
From there, if the neighbor is in bounds of the board, we will increment the lives counter if the absolute value of the neighbor cell is one. This will take into account a negative one, meaning we just changed this cell to dead but it was alive when the game started, or a positive one meaning the cell was alive when the game started and is still alive.
if in_bounds(next_row, next_col):
if abs(board[next_row][next_col]) == 1:
lives += 1
Once we have counted the lives of the neighbors of the given cell, we will return it.
return lives
The last helper function we will make will let us know if the current cell is dead or alive.
It will take a row and column coordinate, an account of alive neighbors of the current cell, and the current state of the cell.
def dead_or_alive(row:int, col:int, lives:int, now:int) -> int:
We will first determine if the current cell is alive if it has the value of one.
alive = board[row][col] == 1
Then, we will determine if we need to change the value of the current cell based on the rules given.
Any live cell with fewer than two live neighbors dies as if caused by under-population.
if alive and lives < 2:
return -1
Any live cell with more than three live neighbors dies, as if by over-population.
elif alive and lives > 3:
return -1
Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
elif not alive and lives == 3:
return 2
If not any of these three scenarios, the cell will retain its current life status and we will return what it is now.
else:
return now
Now we just need to make our two scans through the grid.
For the first scan, for each cell, we will get the state of what the cell is now, how many of the neighbors are alive, and use that to determine whether the current cell is dead or alive.
for row in range(m):
for col in range(n): now = board[row][col]
lives = count_neighbors(row,col)
board[row][col] = dead_or_alive(row, col, lives, now)
For the second scan, for each cell, if the cell is greater than zero then it is one, meaning it was alive and unchanged, or two, meaning it was dead and is now alive at the game's end, so we will mark the cell as alive.
for row in range(m):
for col in range(n):
if board[row][col] > 0:
board[row][col] = 1
Otherwise, the cell was already dead and is zero, or became dead and is now a negative one, either way, we will mark the cell as dead.
else:
board[row][col] = 0