Problem Description
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:
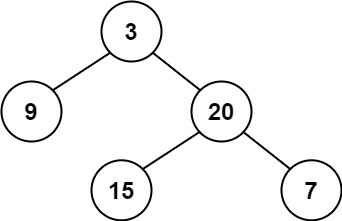
Input: root = [3,9,20,null,null,15,7] Output: true
Example 2:
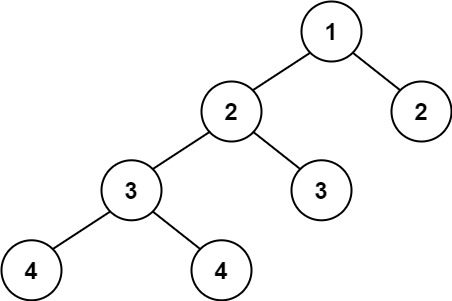
Input: root = [1,2,2,3,3,null,null,4,4] Output: false
Example 3:
Input: root = [] Output: true
Constraints:
- The number of nodes in the tree is in the range
[0, 5000]. -10^4 <= Node.val <= 10^4
The description was taken from https://leetcode.com/problems/balanced-binary-tree/.
Problem Solution
#O(N) Time, O(N) Space
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def postorder(node: TreeNode) -> list:
if not node:
return [True, 0]
left, right = postorder(node.left), postorder(node.right)
curr_balanced = abs(left[1] - right[1]) < 2
prev_balanced = left[0] and right[0]
return [curr_balanced and prev_balanced, 1 + max(left[1],right[1])]
return postorder(root)[0]
Problem Explanation
When doing binary tree questions, it is important to ask "whose information do we need first?" This will let us know whether to perform a preorder traversal if we need the root first, an inorder traversal if we need to traverse the values inorder with the left side first, or a postorder if we need to visit children before parents.
In order to see if the tree is balanced, we will need to get the height of each node. The height of a node isn't how close to the root a node is, but how many nodes are below it as children. The most intuitive way to obtain the height of each node would be to perform a postorder traversal, a traversal where the parent is traversed after the children so that by the time our DFS arrives back up at a node, we will have information on the children.
The information we need from the children of each node is the height so that we can determine if it is balanced, but we will also need to know if each previous child node was balanced as well.
What we will do is perform a postorder traversal on the tree, check if the left and right children of each node are balanced, and if each previous child node was balanced as well, then we will return those answers in a two-index array to each parent node.
Let's start by initializing our recursive, postorder function.
def postorder(node: TreeNode) -> list:
Being a recursive function, we need to make sure that our base case is set so we avoid a stack overflow.
The base case will be if we hit a null node, we will return true that this node is balanced, since it will also have two null children which are balanced, and a height of zero, since there are no child nodes.
if not node:
return [True, 0]
If we are not at a null node, we will recurse the left, then right children.
left, right = postorder(node.left), postorder(node.right)
Once our Depth-First Search yoyo comes back up to the current node after visiting its children, we will check the height of both child nodes.
We will know the current node is balanced if the heights from the second index returned only differ by at most one child.
curr_balanced = abs(left[1] - right[1]) < 2
We will know that each previous node is balanced if they returned true in the first index.
prev_balanced = left[0] and right[0]
Once we have gathered that information, we will return that both the current node and previous child nodes were balanced, and the current height.
return [curr_balanced and prev_balanced, 1 + max(left[1],right[1])]
We take the max between them because if we had two children on one branch and one child on the other, we would be as tall as the two children, plus our current node.
Now that our function is built, we just need to return the first index returned to the root, which will tell us if the root is balanced and all of its children were balanced.
return postorder(root)[0]