Problem Description
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return the maximum area of an island in grid. If there is no island, return 0.
Example 1:
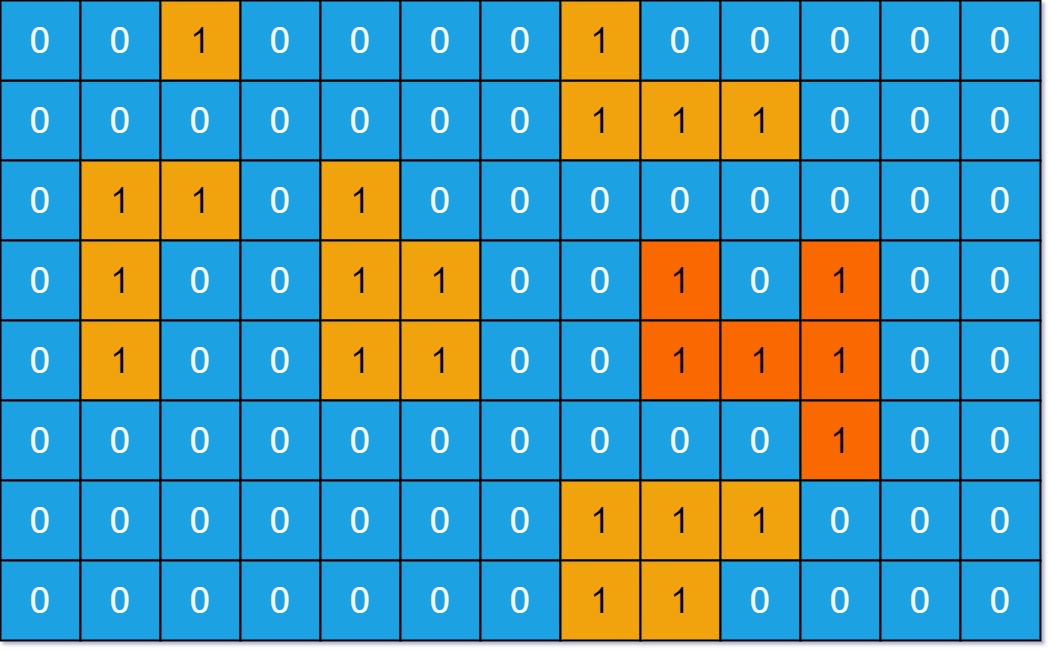
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] Output: 6 Explanation: The answer is not 11, because the island must be connected 4-directionally.
Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]] Output: 0
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]is either0or1.
The description was taken from https://leetcode.com/problems/max-area-of-island/.
Problem Solution
#O(N*M) Time, O(N*M) Space
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
m, n = len(grid[0]), len(grid)
max_island = 0
def land(row:int, col:int)-> bool:
if row < 0 or col < 0 or row >= n or col >= m:
return False
if grid[row][col] == 0:
return False
return True
def dfs(row:int, col:int) -> int:
if not land(row, col):
return 0
grid[row][col] = 0
left = dfs(row, col - 1)
right = dfs(row, col + 1)
up = dfs(row - 1, col)
down = dfs(row + 1,col)
return 1 + left + right + up + down
for row in range(n):
for col in range(m):
if grid[row][col] == 1:
max_island = max(max_island, dfs(row, col))
return max_islandProblem Explanation
This solution will be the same as Number of Islands.
The only additional thing we will need to do is count each piece of land that we visit when we run a Depth-First Search on an island.
The solution is as follows: we will traverse the grid and if we see an island we will run a DFS on that cell. In the DFS, if we have a zero or an out of bounds coordinate, we will return. Otherwise, we will sink the piece of land and increase our count by one then continue the DFS on the upper, lower, left, and right neighbors. Once we are finished with the DFS for an island, we will compare the count of land cells with the current maximum count we have saved. Once we have traversed the entire grid, we will return the maximum count.
Let's start by calculating the length and width of the island, m and n, so that we don't have to calculate this in each DFS call.
m, n = len(grid[0]), len(grid)
We will also initialize our island size running maximum.
max_island = 0
Next, we will make a helper function to aid us in our DFS.
This function will return false if we have gone outside the bounds of the grid, or have hit the water. Otherwise, it will return true.
def land(row:int, col:int)-> bool:
if row < 0 or col < 0 or row >= n or col >= m:
return False
if grid[row][col] == 0:
return False
return True
Next, we will create our recursive, DFS function.
def dfs(row:int, col:int) -> int:
The base case is if the current cell is not land, we will return zero because it will not increase the size of the island at all.
if not land(row, col):
return 0
Otherwise, we will sink this piece of land by setting the value to zero, thus marking it as seen, and we will recurse each of the neighbors. We only want to search these four and not the four diagonals because an island has to be connected four-directionally according to the description.
grid[row][col] = 0
left = dfs(row, col - 1)
right = dfs(row, col + 1)
up = dfs(row - 1, col)
down = dfs(row + 1,col)
Once we have gotten the count from all of the neighbors, which will be given to us once their recursive calls have hit not land, we will take their counts and add one to it to include the current cell, then return the count.
return 1 + left + right + up + down
Now that we have our helper functions built, the rest is easy for us.
We will traverse each row in the grid and each column in the row.
for row in range(n):
for col in range(m):
If we see a piece of land, we will run a DFS on it to get the count of the land pieces that are on the island. We will compare that count with the maximum island count we have so far, and make it the new maximum island if it is greater.
if grid[row][col] == 1:
max_island = max(max_island, dfs(row, col))
Once we have traversed the grid, we will return the maximum island we found.
return max_island