Word Search II

Patrick Leaton

Published: Aug. 7, 2021, 7:51 p.m.

Problem Description

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

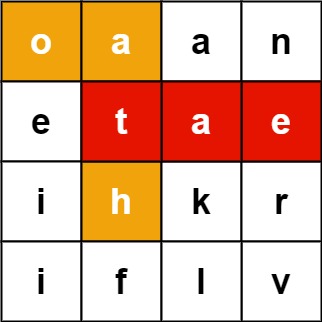
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

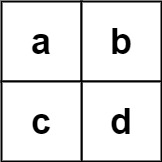
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] is a lowercase English letter.
1 <= words.length <= 3 * 10^4
1 <= words[i].length <= 10
words[i] consists of lowercase English letters.
All the strings of words are unique.

The description was taken from https://leetcode.com/problems/word-search-ii/.

Problem Solution

#O(B*(4*3^L-1)) Time, Where B is board area and L is maximum length of words.

#O(N) Space

class TrieNode:

    def __init__(self, val:int) -> None:

        self.val = val

        self.children = {}

        self.end_here = False

        self.word = None

        

class Solution:               

    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:

        

        def insert(word:str) -> None:

            curr_node = root

            for char in word:

                if char not in curr_node.children:

                    curr_node.children[char] = TrieNode(char)

                curr_node = curr_node.children[char]

            curr_node.end_here = True

            curr_node.word = word

        

        def in_bounds(board:List[List[str]], row:int, col:int) -> bool:

            if row < 0 or row >= len(board) or col < 0 or col >= len(board[0]):

                return False

            else:

                return True

        

        def backtrack(row:int, col:int, parent:TrieNode) -> None:

            char = board[row][col]

            curr_node = parent.children[char]

            if curr_node.end_here:

                if curr_node.word:

                    output.append(curr_node.word)

                    curr_node.word = None

                    

            board[row][col] = "#"

            neighbors = [(-1,0), (1,0), (0,-1), (0,1)]

            for neighbor in neighbors:

                next_row, next_col = row+neighbor[0], col+neighbor[1]

                if not in_bounds(board, next_row, next_col):

                    continue

                if not board[next_row][next_col] in curr_node.children:

                    continue

                backtrack(next_row, next_col, curr_node)

        

            board[row][col] = char

            if not curr_node.children:

                del parent.children[char]

            

        root = TrieNode(None)

        output = []

        for word in words:

            insert(word)

        for row in range(len(board)):

            for col in range(len(board[0])):

                if board[row][col] in root.children:

                    backtrack(row, col, root)

        return output

Problem Explanation

This question is going to have a similar approach to the first Word Search.

The difference is instead of searching for one word, we will be searching for multiple. Because we are searching for multiple words, we are going to need a data structure that will allow us to do this in linear time. If we just tried looking through the input wordlist, that wouldn't be a problem if each word started differently. However, if words share the same prefix then we'd likely begin a search through one until we found a different character than we were expecting and have to start all over again at the next word.

To make this more efficient, we will use a Prefix Tree, a Trie. This way, once we start searching for a prefix, we will reach the end of the word if we find it on the board and not have to start over.

We will make a Trie, push each word into it, then perform a Depth-First Search on the board once we stumble upon a character that is at the root of our Trie. If we keep getting neighbor cells that line up with the Trie path we are on, we will continue the DFS. Once we have traversed the board, we will have a list of values that we found that were also in our Trie.

Let's start by creating our TrieNode class.

Each Trie node will have a character value, a list of children, an attribute to let us know where the end of a word is, and the word itself for easy access.

class TrieNode: def __init__(self, val:int) -> None: self.val = val self.children = {} self.end_here = False self.word = None

In the function we were given, let's create a few helper functions.

The first will be the insert function that we will use to insert nodes into our Trie.

We will set the current node pointer to the root, and then for each character in the word, if the character doesn't already exist inside an existing shared prefix that we have in our Trie, we will create a new node with the character and slap it on the end of this new prefix that we are creating.

def insert(word:str) -> None: curr_node = root for char in word: if char not in curr_node.children: curr_node.children[char] = TrieNode(char)

Once we have the character in the current node's children, if it wasn't already, we will iterate to it.

curr_node = curr_node.children[char]

Once we have finished inserting the word into our Trie, we will put a flag saying that the current prefix ends here, then we will attach the word itself so once we reach the end of the path, we will be able to access the word in constant time.

curr_node.end_here = True curr_node.word = word

Next, we will make a in_bounds function for our DFS to avoid index out-of-bounds errors.

def in_bounds(board:List[List[str]], row:int, col:int) -> bool:

If the row is less than or greater than the length of the board, we will return false. Similarly, if the column is less than or greater than the width of the board, we will return false.

if row < 0 or row >= len(board) or col < 0 or col >= len(board[0]): return False

Otherwise, we will return true.

else: return True

Next, we will make our recursive, backtrack function.

def backtrack(row:int, col:int, parent:TrieNode) -> None:

The current character will be the current cell on the board.

char = board[row][col]

The current node is the node that was instantiated in the parent's children when we inserted it into the Trie.

curr_node = parent.children[char]

If we see the flag that indicates the prefix ends here, we will see if we have the current word here as well.

If we do, we will append it to the output and remove it so that we don't have duplicates if we stumbled on this prefix a second time.

if curr_node.end_here: if curr_node.word: output.append(curr_node.word) curr_node.word = None

This part is a generic backtracking algorithm.

We will mark the cell as seen, create a list of neighbors, the top, bottom, left, and right cells, and prepare the neighbors for a DFS continuation.

board[row][col] = "#" neighbors = [(-1,0), (1,0), (0,-1), (0,1)] for neighbor in neighbors: next_row, next_col = row+neighbor[0], col+neighbor[1]

If the current neighbor isn't in bounds, we will continue to the next and not continue down that DFS path.

if not in_bounds(board, next_row, next_col): continue

If the current neighbor doesn't extend the current prefix, then there is no use going down that DFS path either.

if not board[next_row][next_col] in curr_node.children: continue

If we have a neighbor that is in bounds and contains the next letter of a word that are searching for, we will continue down that DFS path.

backtrack(next_row, next_col, curr_node)

Once the DFS has sprung back to the current function call, we will reset the current cell to what it was in case we need to return to this character later for a different word.

board[row][col] = char

This part is an optimization but is not required. If we have a leaf node, then we can remove it from our Trie to shrink the search space for any future words. If the node is the end of a prefix, we would have already appended it to the output previously in the function so there is no need to continue back down this path.

if not curr_node.children: del parent.children[char]

Now that we have our helper functions built, we just need to make our initial sweep across the board.

We will create a root node and initialize an output first.

root = TrieNode(None) output = []

Next, we will insert all the words into the Trie.

for word in words: insert(word)

After we will iterate through the board and if we find the first character of any word from the wordlist, we will begin our DFS on that cell.

for row in range(len(board)): for col in range(len(board[0])): if board[row][col] in root.children: backtrack(row, col, root)

Once we have finished searching the board, we will return the list of words that we found in it.

return output