Problem Description
You are painting a fence of n posts with k different colors. You must paint the posts following these rules:
- Every post must be painted exactly one color.
- There cannot be three or more consecutive posts with the same color.
Given the two integers n and k, return the number of ways you can paint the fence.
Example 1:
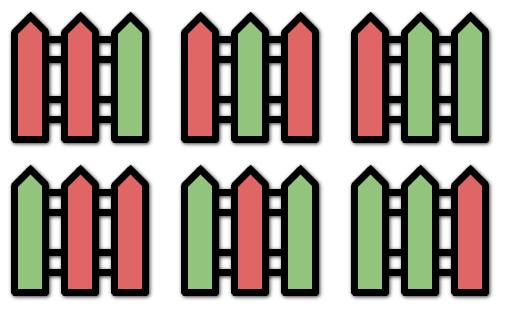
Input: n = 3, k = 2 Output: 6 Explanation: All the possibilities are shown. Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.
Example 2:
Input: n = 1, k = 1 Output: 1
Example 3:
Input: n = 7, k = 2 Output: 42
Constraints:
1 <= n <= 501 <= k <= 105- The testcases are generated such that the answer is in the range
[0, 2^31 - 1]for the givennandk.
The description was taken from https://leetcode.com/problems/paint-fence/.
Problem Solution
#O(N) Time, O(N) Spaceclass Solution: def numWays(self, n: int, k: int) -> int: one_wood, two_wood = k, k**2 if n == 1: return one_wood if n == 2: return two_wood dp = [0]*(n+1) dp[1] = one_wood dp[2] = two_wood for i in range(3, len(dp)): dp[i] = (k-1)*(dp[i-1]+dp[i-2]) return dp[-1]Problem Explanation
This problem is a variation of Climbing Stairs.
Like Climbing Stairs, Decode Ways, Unique Paths, House Robber, this problem falls in the Dynamic Programming category of finding a running combination. To solve these problems, we will arrive at point B and look back at each potential point A that we got here from then add the combinations from point A to point B.
In this case, we have two options, so we will have two point A's for a fence-board we'd like to paint. We could either paint it the same color as the previous board, or we could paint it a different color than the board two places back since a fence can't have three boards of the same color.
We will take the combinations from those two subproblems, and that is how we will determine the final result.
Breaking this problem down into its most simple input, we would have one piece of wood.
With that one piece, we could paint it any color from the number of colors we have because we don't have to worry about having three pieces of the same color.
If we had two pieces, we could choose to paint them the same, or different, for each color. That would be k^2, where k is the number of colors we have.
one_wood, two_wood = k, k**2
If we have those base cases as an input, we will return those combinations.
if n == 1: return one_wood if n == 2: return two_wood
If our input is greater than two, we will need to start storing the combinations in a dp cache.
Index zero will hold the combinations for if n is zero, which would be zero. Index one if n is one, index two if n is two, etc. This is how we will break this problem up into subproblems.
dp = [0]*(n+1) dp[1] = one_wood dp[2] = two_wood
Now, until we get to the total number of wood pieces, we will keep counting three pieces at a time. We have the current board, the previous board, and the board two places behind.
The number of paint combinations we will have is one less than the total number of colors, multiplied by the number of combinations to paint the previous board and the board two boards behind. The reason for this is whatever color we pick for one board, we will have one less color to pick from to paint the board two places to the right. We will end up with a similar calculation for the base case of having two pieces of wood, we can choose to paint the current two pieces of wood the same or different, making it one_wood*two_wood for the combinations, but one of these will have to be with one less color since we can't have three colors in a row.
for i in range(3, len(dp)): dp[i] = (k-1)*(dp[i-1]+dp[i-2])
Once we have reached the nth piece of wood, and we have carried over each additional combination entry into the dp cache, we will return the answer we've been looking for.
How many combinations for the nth piece?
return dp[-1]
Additional Notes
one_wood combination count to the two_wood count, then saving the cumulative count as the two_wood count for the next iteration.#O(N) Time, O(1) Spaceclass Solution: def numWays(self, n: int, k: int) -> int: one_wood, two_wood = k, k**2 if n == 1: return one_wood if n == 2: return two_wood for i in range(3, n+1): one_wood, two_wood = two_wood, (k-1)*(one_wood+two_wood) return two_wood