Count Good Nodes in Binary Tree

Patrick Leaton

Published: Aug. 4, 2021, 5:18 p.m.

Problem Description

Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X.

Return the number of good nodes in the binary tree.

Example 1:

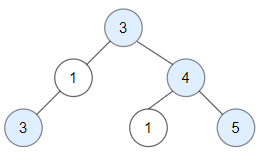
Input: root = [3,1,4,3,null,1,5]
Output: 4
Explanation: Nodes in blue are good.
Root Node (3) is always a good node.
Node 4 -> (3,4) is the maximum value in the path starting from the root.
Node 5 -> (3,4,5) is the maximum value in the path
Node 3 -> (3,1,3) is the maximum value in the path.

Example 2:

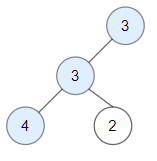
Input: root = [3,3,null,4,2]
Output: 3
Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.

Example 3:

Input: root = [1]
Output: 1
Explanation: Root is considered as good.

Constraints:

The number of nodes in the binary tree is in the range [1, 10^5].
Each node's value is between [-10^4, 10^4].

The description was taken from https://leetcode.com/problems/count-good-nodes-in-binary-tree/.

Problem Solution

#Recursive DFS

#O(N) Time, O(N) Space

class Solution:

def goodNodes(self, root: TreeNode) -> int:

count = 0

def dfs(node: TreeNode, curr_max:int) -> int:

nonlocal count

if not node:

return

if curr_max <= node.val:

count += 1

curr_max = node.val

dfs(node.left, curr_max)

dfs(node.right, curr_max)

return count

return dfs(root, -10**4-1)

#Iterative BFS

#O(N) Time, O(N) Space

class Solution:

def goodNodes(self, root: TreeNode) -> int:

def bfs(root: TreeNode) -> int:

count = 0

if not root:

return 0

queue = collections.deque([(root, -10**4-1)])

while queue:

width = len(queue)

for _ in range(width):

node, curr_max = queue.popleft()

if curr_max <= node.val:

count+=1

curr_max = node.val

if node.left:

queue.append((node.left, curr_max))

if node.right:

queue.append((node.right, curr_max))

return count

return bfs(root)

Problem Explanation

Recursive DFS

Based on the problem description, a node is a "good node" if it is the current maximum node in the path to get there.

The most straightforward way to solve this is to implement a Depth-First Search and as we get to each node, we will check if it is greater than the current maximum. If it is, this is a good node so we will increase the count of good nodes by one and make the current node the current maximum then continue the search on the node's children.

Once we have traversed the tree, we will return the count of good nodes we found in each of our DFS paths.

Let's start by initializing our count.

It will make things easier for us to track this if we store this in the parent function instead of passing it recursively to each node.

count = 0

Next, we will make our recursive, dfs function.

def dfs(node: TreeNode, curr_max:int) -> int:

Within our DFS function, we will initialize our nonlocal count. In Python, this specifies that this new count variable's scope expands beyond this inner function.

nonlocal count

Being a recursive function, let's remember to set the base case.

The base case will be hit if we encounter a null node. If that's the case, we are done searching a path and will return from it.

if not node:

return

Otherwise, we will consider this node as a good node.

If the current max is less than or equal to the current node's value, this node is the current maximum in the path taken to arrive at it. If that is the case, we will increment the count and set the current max as the current node's value.

if curr_max <= node.val:

count += 1

curr_max = node.val

We will continue the DFS on the current node's children and return the count once the DFS yoyo has come back up to the current function.

dfs(node.left, curr_max)

dfs(node.right, curr_max)

return count

Now that we have our DFS function built, we just need to make the initial call by passing the root and a low value outside the bounds of the given constraints as the current max so that it is guaranteed to be overwritten later.

return dfs(root, -10**4-1)

Iterative BFS

The idea is exactly the same as the recursive version but we're swapping out a call stack for a queue data structure to perform a Breadth-First Search.

Let's start by making our iterative, bfs function.

def bfs(root: TreeNode) -> int:

We will need a count of good nodes, same as before.

count = 0

If we have no root, then we have no count of good nodes.

if not root:

return 0

If we have a root, it will be the first to go in the queue, along with a low value outside the bounds of the given constraints as the current max so that it is guaranteed to be overwritten later.

queue = collections.deque([(root, -10**4-1)])

While we still have nodes in the queue to count, we will continue our BFS.

while queue:

Let's start each BFS iteration off by calculating the width of the queue. This is important because it will tell us how many nodes are in the level that we need to look at.

width = len(queue)

For each node in the level, we will pop it off the queue with the current max.

for _ in range(width):

node, curr_max = queue.popleft()

if curr_max <= node.val:

count += 1

curr_max = node.val

If the current node has children in the next level we are going to visit after this one, we will add it to the queue with the current max.

if node.left:

queue.append((node.left, curr_max))

if node.right:

queue.append((node.right, curr_max))

Once we have visited each node in the tree, we will return the number of good nodes we found.

return count

Now that our bfs function is built, we just need to make the initial function call by passing the root node.

return bfs(root)