Problem Description
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
An island is considered to be the same as another if and only if one island can be translated (and not rotated or reflected) to equal the other.
Return the number of distinct islands.
Example 1:
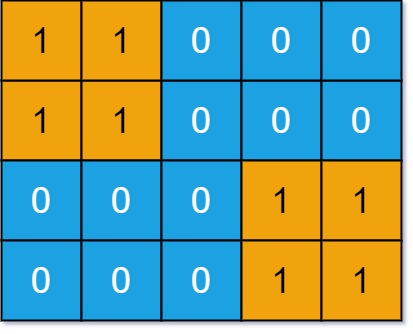
Input: grid = [[1,1,0,0,0],[1,1,0,0,0],[0,0,0,1,1],[0,0,0,1,1]] Output: 1
Example 2:
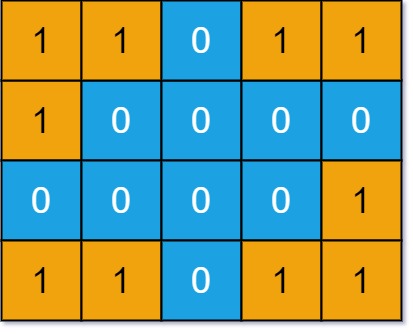
Input: grid = [[1,1,0,1,1],[1,0,0,0,0],[0,0,0,0,1],[1,1,0,1,1]] Output: 3
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]is either0or1.
The description was taken from https://leetcode.com/problems/number-of-distinct-islands/.
Problem Solution
#O(M*N) Time, O(M*N) Space
class Solution:
def numDistinctIslands(self, grid: List[List[int]]) -> int:
distinct_paths = set()
def land(row:int, col:int)-> bool:
if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]):
return False
if grid[row][col] == 0:
return False
return True
def dfs(row:int, col:int, direction:str) -> str:
if not land(row, col):
return "<-"
grid[row][col] = 0
up = dfs(row-1, col, "W")
down = dfs(row+1, col, "S")
left = dfs(row, col-1, "A")
right = dfs(row, col+1, "D")
return direction + up + down + left + right
for row in range(len(grid)):
for col in range(len(grid[0])):
if grid[row][col] == 1:
path = dfs(row, col, "Enter")
distinct_paths.add(path) return len(distinct_paths)Problem Explanation
This problem is a slightly more difficult version of Number of Islands.
We are still going to run a Depth-First Search on any surrounding land each time we encounter a piece of land, but we need to track islands that are the exact same in shape and not count them in our final answer.
W to go up, S to go down, A to go left, and D to go right. If we hit water or go out of bounds, we will hit <-. By doing this, we can track the exact order of keystrokes it took to sink an island. That way, if we encounter the same combinations later, we will know that it was the same island.
We can use a hashset to append our combination strings so that way at the end, only the unique combinations will be counted.
Let's initialize our unique_paths set and start by creating our two helper functions.
distinct_paths = set()
The first is a function called land, which will take cell coordinates in the form of a row and column integer.
def land(row:int, col:int)-> bool:
This function will let us know if we have gone out of bounds of the matrix, or have hit the water. In either case, we aren't on land so we will return false.
if row < 0 or col < 0 or row >= len(grid) or col >= len(grid[0]):
return False
if grid[row][col] == 0:
return False
Otherwise, we will return True.
return True
Next, we will create our recursive, dfs function.
This function will take a row, a column, and a direction that was taken to get to the current cell.
def dfs(row:int, col:int, direction:str) -> str:
Being a recursive function, it is important that we establish the base case first.
This base case is if we hit a cell that is not land, we shall return by using a backspace. This way, our DFS can continue sinking every inch of land until it runs out of land to sink.
if not land(row, col):
return "<-"
If the current cell is land, we will sink it by setting it to zero.
grid[row][col] = 0
Then, we will need to sink the entire island so we will start smashing keys.
up = dfs(row-1, col, "W")
down = dfs(row+1, col, "S")
left = dfs(row, col-1, "A")
right = dfs(row, col+1, "D")
Once our DFS function has crawled into each direction sinking each land piece of this island, we will join the initial direction we took to get here with each of the paths that every four directions took into a string. We will return that string to any parent function call.
return direction + up + down + left + right
A typical path will look this like this for a single island DFS traversal: "Enter<-S<-<-<-DW<-<-<-<-<-<-<-<-<-". An enter to begin the DFS, then an S to go down, a bunch of hitting non-land, a D to go right, and a W to go back up to finish traversing a four-square island.
Now that we have our functions built, we just need to start the game.
For each row, and for each column in each row, we will set sails for land.
for row in range(len(grid)):
for col in range(len(grid[0])):
If we spot to land, we will hit enter and begin our DFS on it, looking for booty.
if grid[row][col] == 1:
path = dfs(row, col, "Enter")
Once we have sunk the land, we will make note of our travels in our distinct paths hashmap.
distinct_paths.add(path)
After we have traveled the ocean, we will count the number of unique paths we encountered when sinking islands.
return len(distinct_paths)