Problem Description
You are given an m x n grid rooms initialized with these three possible values.
-1A wall or an obstacle.0A gate.INFInfinity means an empty room. We use the value231 - 1 = 2147483647to representINFas you may assume that the distance to a gate is less than2147483647.
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.
Example 1:
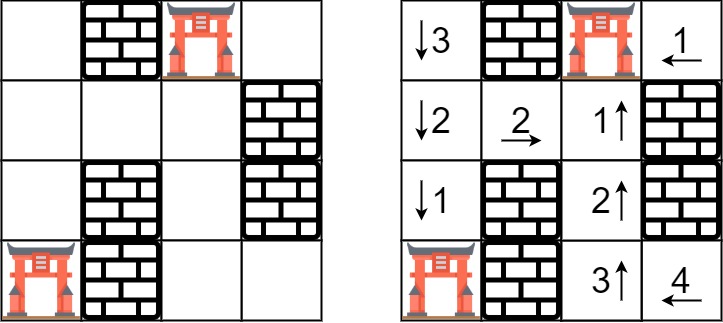
Input: rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]] Output: [[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
Example 2:
Input: rooms = [[-1]] Output: [[-1]]
Example 3:
Input: rooms = [[2147483647]] Output: [[2147483647]]
Example 4:
Input: rooms = [[0]] Output: [[0]]
Constraints:
m == rooms.lengthn == rooms[i].length1 <= m, n <= 250rooms[i][j]is-1,0, or2^31 - 1.
The description was taken from https://leetcode.com/problems/walls-and-gates/.
Problem Solution
#O(M*N) Time, O(M*N) Spaceclass Solution: def wallsAndGates(self, rooms: List[List[int]]) -> None: seen, queue = {}, collections.deque() neighbors = [(0,1), (1,0), (-1,0), (0,-1)] for row in range(len(rooms)): for col in range(len(rooms[0])): if rooms[row][col] == 0: queue.append((row,col)) seen[(row,col)] = True def inbounds(row, col) -> bool: if (row < 0 or row >= len(rooms) or col < 0 or col >= len(rooms[0])): return False if (row, col) in seen or rooms[row][col] == -1: return False return True def bfs() -> None: distance = 0 while queue: width = len(queue) for _ in range(0, width): row, col = queue.popleft() rooms[row][col] = distance for neighbor in neighbors: next_row = row + neighbor[0] next_col = col + neighbor[1] if not inbounds(next_row, next_col): continue queue.append((next_row, next_col)) seen[(next_row,next_col)] = True distance += 1 bfs()Problem Explanation
We have a matrix and each point that isn't a wall or gate needs to be populated with the distance to the closest gate. If we change our perspective, we can view this as a search for the distances from the closest gate.
A search in this manner will look at all surrounding neighbors from each gate, which tells us that this may be solved with a Breadth-First Search.
What we will do is make one scan through the matrix and initialize our queue with the gates. Then, we will perform a BFS on all of the unseen neighbors of the gates, marking them with the current distance increment. After, we will perform a BFS on the neighbors of those cells. This will continue until we have visited each cell.
Let's start by initializing our seen hashmap which will allow us to not keep processing the same cells. We will also initialize our empty queue which we will first fill with gates when we see them later.
seen, queue = {}, collections.deque()
We'll also create this list that holds the distance for the neighbors of each cell within the matrix.
This translates to the neighbor one column to the right, one row down, one column to the left, and one row up from the current cell.
neighbors = [(0,1), (1,0), (-1,0), (0,-1)]
Next, we will traverse each row of the matrix, and each cell in the row, looking for gates. if we find a gate, we will mark the coordinates as seen and add them to our queue.
for row in range(len(rooms)): for col in range(len(rooms[0])): if rooms[row][col] == 0: queue.append((row,col)) seen[(row,col)] = True
Now that we have all of the gates in our queue, we are ready for a BFS.
Before we make our BFS function, however, let's go ahead and create a helper function to check the validity of each cell before we process it,
This function will check whether we have already seen the cell, if the cell is a gate, or if the cell is out of bounds. It will return false if any of those cases are true, otherwise, it will return true and we have the green light to process the cell whose coordinates were passed into the function.
def inbounds(row, col): if (row < 0 or row >= len(rooms) or col < 0 or col >= len(rooms[0])): return False if (row, col) in seen or rooms[row][col] == -1: return False return True
Now we can finally make our bfs function.
def bfs() -> None:
We will start off by setting the initial distance of the function to zero.
distance = 0
Now we just have a traditional BFS.
While the queue still has cells to process, we haven't processed all of the cells and will continue our BFS.
while queue:
We will start each iteration off by calculating the width of the queue. This lets us know how many cells are within the given layers before we start adding in anymore from the next layer.
width = len(queue)
Now we will start processing the cells for the current layers we have around the gates.
for _ in range(0, width):
We will start by popping a row and column coordinate from the queue and mark the cell at that coordinate with the current distance increment.
row, col = queue.popleft() rooms[row][col] = distance
Then, we will use those same coordinates to get the neighbors of that cell from the neighbors list we made previously.
This gives us the coordinates of each neighbor one column to the right, one row down, one column to the left, and one row up.
for neighbor in neighbors: next_row = row + neighbor[0] next_col = col + neighbor[1]
For each of those neighbors, we will check if they are in-bounds and unseen. If they are, we will visit them next by adding them to our queue and marking them as seen. If not, we will continue for each of the ones that are not.
if not inbounds(next_row, next_col): continue queue.append((next_row, next_col)) seen[(next_row,next_col)] = True
Once we have finished processing cells within the width of the queue we had at the beginning of the iteration, we have completed a search for a layer from the gates. Now we will increment the distance and anticipate searching the next layer.
distance += 1
When our queue is empty, that means that we have processed each cell from the matrix.
Now that our BFS function is made, we just need to make the initial call to fill in the distance from each gate.
bfs()