Problem Description
You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).
There is at least one empty seat, and at least one person sitting.
Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.
Return that maximum distance to the closest person.
Example 1:
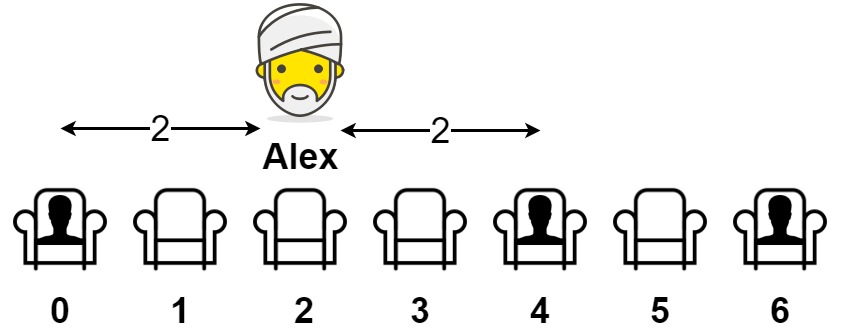
Input: seats = [1,0,0,0,1,0,1] Output: 2 Explanation: If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2. If Alex sits in any other open seat, the closest person has distance 1. Thus, the maximum distance to the closest person is 2.
Example 2:
Input: seats = [1,0,0,0] Output: 3 Explanation: If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away. This is the maximum distance possible, so the answer is 3.
Example 3:
Input: seats = [0,1] Output: 1
Constraints:
2 <= seats.length <= 2 * 10^4seats[i]is0or1.- At least one seat is empty.
- At least one seat is occupied.
The description was taken from https://leetcode.com/problems/maximize-distance-to-closest-person/.
Problem Solution
#O(N) Time, O(1) Spaceclass Solution: def maxDistToClosest(self, seats: List[int]) -> int: left, right = 0, len(seats) -1 left_count, right_count = 0, 0 middle_count, running_count = 0, 0 while left < right: if seats[left] == 0: left_count += 1 left += 1 elif seats[right] == 0: right_count += 1 right -= 1 else: break for i in range (left, right): if seats[i] == 0: running_count += 1 middle_count = max(middle_count, running_count) else: running_count = 0 return max(left_count, right_count, ((middle_count + 1)//2))Problem Explanation
This problem comes down to accounting for vacant edge seats and vacant middle seats. The edge seats have the benefit of not having occupied seats before their edge so we can count them first using two pointers, one for each edge moving inward. Then, once we have accounted for each vacant seat at the ends, we will count the middle seats between the indices where the pointers stopped.
Let's start by initializing the left and right pointers to the first and last indices of the input array.
left, right = 0, len(seats) -1
We'll then set our counters for the left, right, and middle seats, as well as the running count that we will use to count consecutive middle seats.
left_count, right_count = 0, 0 middle_count, running_count = 0, 0
As far as the distance for vacant seats on the end of the isles goes, the distance will be k, unlike seats in the middle which will be k+1//2. What this means is if Alex were to sit in the seat on the very left side, he would only have to worry about taken seats to the right of him, the same goes for the other side. Knowing this, we can just count the number of consecutive seats at the ends and directly convert these to distances one-for-one.
We will use our left and right pointers to count these seats and we will break from our loop once the pointers overlap or we have no more vacant seats to count on the ends.
while left < right:
If the element at the left index is a vacant seat, we will increment our left counter and move the left pointer to the right by one.
if seats[left] == 0: left_count += 1 left += 1
We will do the same for the right if it is a vacant seat.
elif seats[right] == 0: right_count += 1 right -= 1
If neither end has seats that are vacant, we will break from our loop and begin counting the middle seats.
else: break
We just counted the number of seats at the ends, so we will count the seats in the middle, between the left and right pointer.
for i in range (left, right):
If the current seat is vacant, we will increment our running count and see if the running count is higher than the maximum middle count we have stored.
if seats[i] == 0: running_count += 1 middle_count = max(middle_count, running_count)
If the seat isn't vacant, we will reset our count because we are looking for the maximum consecutive seats that we can find.
else: running_count = 0
Once we have finished counting the middle seats, we will return the maximum distance from either the left count, right count, or middle count, (( middle count + 1)//2)).
return max(left_count, right_count, ((middle_count + 1)//2))
The reason we calculate this (k+1)//2 distance is because if we have three consecutive seats, Alex will need to worry about somebody sitting next to him on both the right and the left sides.
Let's take this test case for example [1,0,0,0,1]. If Alex picks the middle seat then he only has one empty seat from the two people next to him on both sides.
((3+1) // 2) is a distance of two seats.