Problem Description
You are given an m x n grid where each cell can have one of three values:
0representing an empty cell,1representing a fresh orange, or2representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example 1:
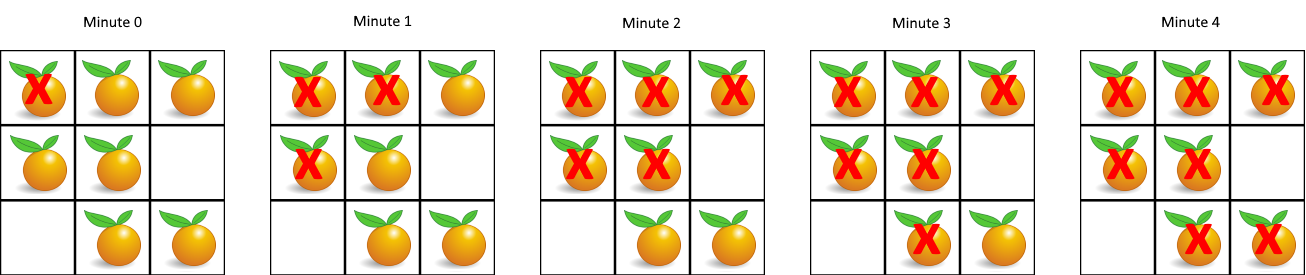
Input: grid = [[2,1,1],[1,1,0],[0,1,1]] Output: 4
Example 2:
Input: grid = [[2,1,1],[0,1,1],[1,0,1]] Output: -1 Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:
Input: grid = [[0,2]] Output: 0 Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]is0,1, or2.
The description was taken from https://leetcode.com/problems/rotting-oranges/.
Problem Solution
#O(M*N) Time, O(M*N) Spaceclass Solution: def orangesRotting(self, grid: List[List[int]]) -> int: rotten, fresh = {}, {} minutes = 0 neighbors = [(0,1), (1,0), (-1,0), (0,-1)] for row in range(len(grid)): for col in range(len(grid[0])): if grid[row][col] == 1: fresh[(row,col)] = True if grid[row][col] == 2: rotten[(row,col)] = True while len(fresh) > 0: infected = {} for orange in rotten: row, col = orange[0], orange[1] for neighbor in neighbors: next_row = row + neighbor[0] next_col = col + neighbor[1] if (next_row, next_col) in fresh: del fresh[(next_row, next_col)] infected[(next_row, next_col)] = True if not infected: return -1 rotten = infected minutes += 1 return minutesProblem Explanation
If we view the rotting process, we can see that it travels outward within a sonar-type fashion through each minute.
That motion is going to be more of a Breadth-First Search than a Depth-First Search where it would go to the farthest orange toward the bottom before coming up to infect the other oranges around it.
What we can do is use one dictionary to track the rotten oranges and one to track the fresh oranges. Then, we will go through the list of rotten oranges and see if their neighbors are fresh. If they are, then they are now infected so we'll delete those fresh oranges from their fresh list and add them to an infected list. We will continue this until there are no more oranges within our fresh list.
Each BFS traversal iteration is one minute.
Let's start by initializing our rotten and fresh lists and our running, minutes tracker.
rotten, fresh = {}, {} minutes = 0
We'll also create this list that holds the distance for the neighbors of each cell within the matrix.
This translates to the neighbor one column to the right, one row down, one column to the left, and one row up from the current cell.
neighbors = [(0,1), (1,0), (-1,0), (0,-1)]
Then, we will traverse each cell within the matrix and take inventory of our oranges.
for row in range(len(grid)): for col in range(len(grid[0])):
If the orange is a one, it is fresh so we will add it to the fresh list.
if grid[row][col] == 1: fresh[(row,col)] = True
If the orange is a two, it is rotten so we will add it to the rotten list.
if grid[row][col] == 2: rotten[(row,col)] = True
Then, while the length of the fresh dictionary is greater than zero, we still have fresh oranges we are waiting to rot.
while len(fresh) > 0:
We'll make a new list of infected oranges that are fresh oranges that are neighbors to the rotten oranges that we know are about to become rotten.
infected = {}
Now we'll continuously look through each orange in the rotten list.
for orange in rotten:
The row and column coordinates of each matrix cell are the first and second index, respectively.
row, col = orange[0], orange[1]
We'll use each orange in the rotten list's row and column values to see where each neighbor is. This gives us the coordinates of each neighbor one column to the right, one row down, one column to the left, and one row up.
for neighbor in neighbors: next_row = row + neighbor[0] next_col = col + neighbor[1]
If we find those coordinates in the fresh list, that means we have a fresh neighbor that is by a rotten orange, so it is now infected.
if (next_row, next_col) in fresh:
If that is the case, we will delete it from the fresh list and add it to the infected list.
if (next_row, next_col) in fresh: del fresh[(next_row, next_col)] infected[(next_row, next_col)] = True
At this point, if we have no infected oranges, we had no fresh oranges that were right by rotten oranges, in which case the rest of our oranges aren't going to become rotten.
If that is the case, we will return a negative one to signify that the rotting of all oranges is impossible.
if not infected: return -1
If not, our batch of infected oranges is going to be rotten and another minute will elapse each time we go through this process.
rotten = infected minutes += 1
Once we have no more fresh oranges, that means they have all become rotten so we will return the number of minutes, the number of iterations, that had to pass before they all got infected and became rotten.
return minutes